递推算法
递推算法是一种重要的数学方法,在数学的各个领域中都有广泛的运用,也是在计算机数值计算中一个重要的算法。这种算法的特点是:一个问题的求解需要经过一系列的计算,在已知条件和所求问题之间存在某种相互联系的关系。在计算时,如果可以找到前后过程之间的数量关系(即递推式),那么,从问题出发逐步推到已知条件,这种方法叫逆推。无论顺推还是逆推,其关键是要找到递推式。这种处理问题的方法能使复杂运算化为若干步重复的简单运算,充分发挥出计算机擅长于重复处理的特点。
递推算法的首要问题是得到相邻的数据项间的关系(即递推关系)。递推算法避开了求通项公式的麻烦,把一个复杂的问题的求解,分解成了连续的若干步简单运算。一般来说,可以将递推算法看成是一种特殊的迭代算法。
递推关系描述了一个问题的较大实例与其较小实例之间的关系。递推算法广泛应用于各种数学和计算问题,尤其是在处理涉及序列、数组和其他递归结构的问题时。
递推算法的实现通常有两种方式:迭代和递归
# 基本概念
- 递推关系(Recurrence Relation): 递推关系是一种公式,用于表示较大问题实例与较小问题实例之间的关系。常见的递推关系形式如:
- 初始条件(Initial Conditions): 初始条件是递推关系的基础,它定义了一些已知的较小实例的值,这些值用于启动递推过程。例如,斐波那契数列的初始条件为:
# 递推算法的实现步骤
确定递推关系: 确定问题的递推关系,即定义如何通过较小的实例来计算当前实例。
设定初始条件: 设定递推过程的初始条件,确保递推过程有一个启动点。
编写递推算法: 使用迭代或递归的方法实现递推关系。
# 递推算法的C++实现
以下通过几个具体例子来展示如何在C++中实现递推算法。
# 1. 斐波那契数列
斐波那契数列是最经典的递推关系之一,其定义如下:
初始条件:
# 迭代实现
#include <iostream> // 包含输入输出流库
using namespace std; // 使用标准命名空间
// 定义一个函数来计算斐波那契数列的第 n 项
int fibonacci(int n) {
if (n <= 1) return n; // 如果 n 小于等于 1,直接返回 n
int a = 0, b = 1, c; // 初始化三个变量 a, b 和 c,a 和 b 分别表示斐波那契数列的前两项
for (int i = 2; i <= n; ++i) { // 从 2 开始循环到 n
c = a + b; // 计算当前项 c 为前两项之和
a = b; // 更新 a 为 b 的值
b = c; // 更新 b 为 c 的值
}
return c; // 返回第 n 项的值
}
int main() {
int n = 10; // 定义一个整数 n 并赋值为 10
cout << "Fibonacci(" << n << ") = " << fibonacci(n) << endl; // 输出斐波那契数列的第 n 项
return 0; // 返回 0,表示程序正常结束
}
# 递归实现
#include <iostream> // 引入输入输出流库,用于输出数据到控制台
using namespace std; // 使用标准命名空间,简化代码书写
// 定义一个递归函数,用于计算第n个斐波那契数
int fibonacci(int n) {
if (n <= 1) return n; // 如果n是0或1,直接返回n(即斐波那契数的前两个数)
return fibonacci(n - 1) + fibonacci(n - 2); // 否则,返回前两个斐波那契数之和
}
int main() {
int n = 10; // 定义一个整数n,并赋值为10
// 输出第n个斐波那契数
cout << "Fibonacci(" << n << ") = " << fibonacci(n) << endl;
return 0; // 返回0,表示程序正常结束
}
# 2. 阶乘
阶乘的递推关系定义为:
初始条件:
# 迭代实现
#include <iostream> // 包含输入输出流库
using namespace std; // 使用标准命名空间
int factorial(int n) { // 定义计算阶乘的函数,参数为整数n
int result = 1; // 初始化结果为1
for (int i = 2; i <= n; ++i) { // 循环计算从2到n的乘积
result *= i; // 将i乘到结果中
}
return result; // 返回计算结果
}
int main() { // 主函数
int n = 5; // 初始化一个整数n为5
cout << n << "! = " << factorial(n) << endl; // 输出n的阶乘
return 0; // 返回0表示成功结束
}
# 递归实现
#include <iostream> // 包含输入输出流库
using namespace std; // 使用标准命名空间
int factorial(int n) { // 定义一个递归函数,计算阶乘
if (n <= 1) return 1; // 如果 n 小于等于 1,返回 1,防止无限递归
return n * factorial(n - 1); // 递归调用函数,计算 n 的阶乘
}
int main() { // 主函数
int n = 5; // 声明并初始化变量 n
cout << n << "! = " << factorial(n) << endl; // 输出 n 的阶乘
return 0; // 返回主函数的结束状态
}
# 3. 二项式系数(Pascal's Triangle)
基本概念
二项式系数,也称为组合数,表示从 n 个元素中选择 k 个元素的不同组合的数量。它通常表示为
二项式系数在许多数学领域和应用中都有重要作用,包括概率论、统计学、代数等。
# 二项式系数的定义
二项式系数可以用以下公式计算:
其中, n! 表示 n 的阶乘,定义为 n 乘以所有小于 n 的正整数,即:
# Pascal's Triangle(帕斯卡三角形)
Pascal's Triangle 是一种几何排列,它的每一行对应于二项式系数。帕斯卡三角形的特点是,每个数字等于其上方两个数字之和。帕斯卡三角形的前几行如下所示:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
每行的第 n 行表示
二项式系数的递推关系为:
初始条件:
# 迭代实现
#include <iostream> // 包含输入输出流库
#include <vector> // 包含向量容器库
using namespace std; // 使用标准命名空间
int binomialCoefficient(int n, int k) { // 计算二项式系数的函数定义,接受两个整数参数 n 和 k
vector<vector<int>> C(n + 1, vector<int>(k + 1, 0)); // 创建一个二维向量 C,大小为 (n+1) x (k+1),并初始化为全0
for (int i = 0; i <= n; ++i) { // 外层循环遍历 0 到 n
for (int j = 0; j <= min(i, k); ++j) { // 内层循环遍历 0 到 min(i, k)
if (j == 0 || j == i) // 如果 j 等于 0 或者 j 等于 i,即在边界上
C[i][j] = 1; // 则二项式系数为 1
else
C[i][j] = C[i - 1][j - 1] + C[i - 1][j]; // 否则根据组合公式计算二项式系数
}
}
return C[n][k]; // 返回计算得到的二项式系数
}
int main() { // 主函数
int n = 5, k = 2; // 设置 n 和 k 的值
cout << "C(" << n << ", " << k << ") = " << binomialCoefficient(n, k) << endl; // 输出二项式系数的计算结果
return 0; // 返回 0,表示程序正常退出
}
# 递归实现
#include <iostream> // 包含输入输出流库
using namespace std; // 使用标准命名空间
int binomialCoefficient(int n, int k) { // 定义计算二项式系数的函数,参数为 n 和 k
if (k == 0 || k == n) return 1; // 如果 k 等于 0 或者等于 n,返回 1
return binomialCoefficient(n - 1, k - 1) + binomialCoefficient(n - 1, k); // 递归计算二项式系数
}
int main() { // 主函数
int n = 5, k = 2; // 定义并初始化 n 和 k 的值
cout << "C(" << n << ", " << k << ") = " << binomialCoefficient(n, k) << endl; // 输出组合数 C(n, k) 的值
return 0; // 返回 0,表示程序正常结束
}
# 五种典型的递推关系
- 斐波那契数列(Fibonacci Sequence)
- 汉诺塔问题(Tower of Hanoi)
- 平面分割问题(Plane Division Problem)
- Catalan 数(Catalan Numbers)
- 第二类 Stirling 数(Stirling Numbers of the Second Kind)
# 1. Fibonacci 数列
问题提出:
由意大利著名数学家Fibonacci于1202年提出的“兔子繁殖问题”(又称"Fibonacci问题")。假定一对雌雄兔子在两个月后可以繁殖出一对小兔子,问经过n个月后共有多少对兔子。
递推关系:
边界条件:
示例计算:
Fibonacci数列在组合计数和优选法中有广泛的应用,例如“骨牌覆盖”问题。
递推关系推导过程
斐波那契数列是一个以递推方式定义的数列,其递推关系式为:
F(n) = F(n-1) + F(n-2)
其中初始条件为:
F(0) = 0 F(1) = 1
这个递推关系的意思是,从第三项开始,斐波那契数列中的每一个数都是前两个数的和。下面是斐波那契数列的前几项,通过递推关系推导的过程:
初始条件:
F(0) = 0F(1) = 1计算
F(2):F(2) = F(1) + F(0) = 1 + 0 = 1计算
F(3):F(3) = F(2) + F(1) = 1 + 1 = 2计算
F(4):F(4) = F(3) + F(2) = 2 + 1 = 3计算
F(5):F(5) = F(4) + F(3) = 3 + 2 = 5计算
F(6):F(6) = F(5) + F(4) = 5 + 3 = 8计算
F(7):F(7) = F(6) + F(5) = 8 + 5 = 13计算
F(8):F(8) = F(7) + F(6) = 13 + 8 = 21
如此继续下去,你可以用这个递推关系推导出斐波那契数列的任意一项
小练习
问题:
编写一个C++程序,计算并输出第n个月后兔子的总对数(Fibonacci数列)。
代码:
#include <iostream> // 包含标准输入输出流库
using namespace std; // 使用标准命名空间
int fibonacci(int n) { // 定义一个计算斐波那契数列的函数,参数为 n
if (n <= 1) return n; // 如果 n 小于等于 1,返回 n
int a = 0, b = 1, c; // 初始化斐波那契数列的前两项
for (int i = 2; i <= n; ++i) { // 循环计算直到第 n 项
c = a + b; // 计算第 n 项的值
a = b; // 更新前两项的值
b = c; // 更新前两项的值
}
return c; // 返回第 n 项的值
}
int main() { // 主函数
int n; // 声明一个变量 n
cout << "Enter the number of months: "; // 提示用户输入月份数量
cin >> n; // 从标准输入读取用户输入的月份数量
cout << "Number of rabbit pairs after " << n << " months: " << fibonacci(n) << endl; // 输出经过 n 个月后的兔子对数
return 0; // 返回程序执行成功
}
Fibonacci 数列: 使用迭代方法计算Fibonacci数列,避免了递归的高时间复杂度。
# 2. 汉诺塔问题
基本概念
汉诺塔问题是一个经典的数学问题,它涉及到一个传说中的印度寺庙的神龛,称为汉诺塔。问题的描述如下:
在神龛上有三根柱子,分别标记为A、B、C,初始时,所有的盘子都放在柱子A上,从上到下依次按大小顺序排列。问题的目标是将所有的盘子从柱子A移动到柱子C,并且遵循以下规则:
- 每次只能移动一个盘子。
- 盘子可以放在任意一个柱子上,但是不能放在比它小的盘子上面。
- 每次移动都必须遵守盘子的大小顺序。
这个问题的关键是找到一个有效的移动方案,使得所有的盘子最终都从柱子A移动到柱子C,而且在整个过程中都满足上述规则。
汉诺塔问题的解决方案通常使用递归算法,基本思路是将n个盘子的移动分解为三个步骤:
- 将除了最底下的一个盘子以外的所有盘子都从柱子A移动到柱子B。
- 将最底下的盘子从柱子A移动到柱子C。
- 将除了最底下的一个盘子以外的所有盘子都从柱子B移动到柱子C。
这种递归思想可以直观地理解为,将移动n个盘子的问题分解为移动n-1个盘子的子问题。递归的终止条件是当只有一个盘子时,直接将它从柱子A移动到柱子C即可。
整体推导过程:
涉及将一堆盘子从一个柱子移动到另一个柱子,同时遵循以下规则:
- 只能一次移动一个盘子。
- 永远不能将较大的盘子放在较小的盘子上面。
这个问题可以用递归方法来解决,其中递推关系起着关键作用。
假设我们有一个汉诺塔问题,其中有n个盘子。我们用H(n)表示将这些盘子从一根柱子移动到另一根柱子所需的步骤数。
首先,我们将问题分解为以下步骤:
- 将前n-1个盘子从起始柱子移动到中间柱子(利用空闲的柱子作为辅助)。
- 将第n个盘子从起始柱子移动到目标柱子。
- 将前n-1个盘子从中间柱子移动到目标柱子(利用空闲的柱子作为辅助)。
现在,让我们用递推关系来表示这个过程:
- 将前n-1个盘子从起始柱子移动到中间柱子的步骤数为H(n-1)。
- 将第n个盘子从起始柱子移动到目标柱子的步骤数为1。
- 将前n-1个盘子从中间柱子移动到目标柱子的步骤数为H(n-1)。
因此,总步骤数H(n)可以表示为:H(n) = 2H(n-1) + 1
问题提出:
汉诺塔由n个大小不同的圆盘和三根木柱组成,要求将n个盘子从一根柱子移动到另一根柱子上,遵循以下规则:
- 一次只能移动一个圆盘。
- 圆盘只能存放在三根柱子上。
- 任何时候大盘不能压在小盘上。
推演过程:
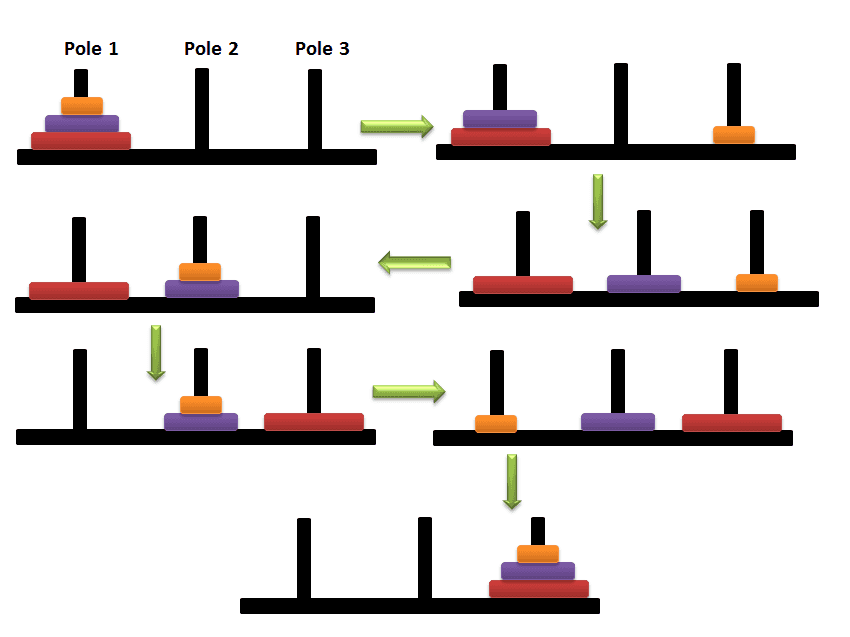
递推关系:
边界条件:
示例计算:
汉诺塔问题是经典的递归问题,广泛用于计算思维训练和算法设计课程中。
递推关系推导过程
汉诺塔问题的目标是将 n 个盘子从一个柱子移动到另一个柱子,遵守以下规则:
- 每次只能移动一个盘子。
- 任何时刻都不能将一个大盘子放在小盘子上面。
为了推导递推关系,我们定义 T(n) 为将 n 个盘子从一个柱子移动到另一个柱子所需的最少移动次数。解决这个问题的步骤如下:
- 将前
n-1个盘子从源柱子移动到辅助柱子。 - 将第
n个盘子从源柱子移动到目标柱子。 - 将前
n-1个盘子从辅助柱子移动到目标柱子。
我们可以分解这个问题:
- 将前
n-1个盘子从源柱子移动到辅助柱子需要T(n-1)次移动。 - 将第
n个盘子从源柱子移动到目标柱子需要 1 次移动。 - 将前
n-1个盘子从辅助柱子移动到目标柱子需要T(n-1)次移动。
所以,总的移动次数 T(n) 可以表示为:
T(n) = T(n-1) + 1 + T(n-1)
这可以简化为:
T(n) = 2T(n-1) + 1
为了完全理解这个递推关系,让我们从 n=1 开始计算:
- 对于
n=1,只需要一次移动,所以T(1) = 1。 - 对于
n=2,需要将第一个盘子移动到辅助柱子,然后将第二个盘子移动到目标柱子,最后将第一个盘子从辅助柱子移动到目标柱子,所以T(2) = 2T(1) + 1 = 2 * 1 + 1 = 3。 - 对于
n=3,我们按照同样的逻辑得到T(3) = 2T(2) + 1 = 2 * 3 + 1 = 7。
我们可以看出,这个关系递归计算每一个 n 都是前一步的两倍加一。
为了更清楚地理解,我们可以展开这个递推公式:
T(n) = 2T(n-1) + 1 T(n-1) = 2T(n-2) + 1 T(n-2) = 2T(n-3) + 1
把这些方程代入,我们得到:
T(n) = 2(2T(n-2) + 1) + 1 = 4T(n-2) + 2 + 1 = 4T(n-2) + 3 T(n) = 4(2T(n-3) + 1) + 3 = 8T(n-3) + 4 + 3 = 8T(n-3) + 7
可以观察到,随着递推次数增加,幂次也在增加。实际上,我们可以归纳出:
T(n) = 2^k T(n-k) + (2^k - 1)
特别地,当 k=n 时,T(n-n) = T(0)。在汉诺塔问题中,0 个盘子需要 0 次移动,所以 T(0) = 0。于是:
T(n) = 2^n T(0) + (2^n - 1) = 0 + 2^n - 1
因此,我们得到汉诺塔问题的最少移动次数为:
T(n) = 2^n - 1
这就是汉诺塔问题的递推关系推导过程及其最终的闭式解。
小练习
问题:
编写一个C++程序,计算并输出将n个盘子从柱子A移动到柱子C所需的最少移动次数。
代码:
#include <iostream> // 包含标准输入输出流的头文件
using namespace std; // 使用标准命名空间
int hanoi(int n) { // 定义递归函数hanoi,用于计算汉诺塔问题的移动次数
if (n == 1) return 1; // 当只有一个盘子时,移动次数为1
return 2 * hanoi(n - 1) + 1; // 汉诺塔移动次数公式:2 * f(n - 1) + 1
}
int main() { // 主函数
int n; // 用于存储用户输入的盘子数量
cout << "Enter the number of disks: "; // 提示用户输入盘子数量
cin >> n; // 从标准输入流中获取用户输入的盘子数量
cout << "Minimum number of moves required: " << hanoi(n) << endl; // 输出移动盘子的最小次数
return 0; // 返回程序执行成功
}
汉诺塔问题: 使用递归方法计算将n个盘子从柱子A移动到柱子C所需的最少移动次数。
# 3. 平面分割问题
基本概念
平面分割问题是一个经典的几何学问题,它涉及在平面上画出一定数量的直线或曲线,使得平面被这些线段分割成了多少个区域的问题。在这个问题中,通常规定这些线段不会相交于三个或更多的点,而且任意两条线段之间只会相交于两个点。
具体来说,平面分割问题通常描述为:给定n条直线(或曲线),求这些线段将平面分割成的区域个数。这里的线段是封闭的,也就是说它们构成了凸多边形,且相交于不同的点。
例如,当有一条直线时,平面被分割成了两个区域;当有两条相交的直线时,平面被分割成了四个区域;当有三条相交的直线时,平面被分割成了七个区域,依次类推。
解决平面分割问题的关键在于找到计算区域个数的递推关系式。通常,可以通过观察规律找到这个递推关系式,然后利用递归或迭代的方式计算区域个数。
问题提出:
有n条封闭曲线画在平面上,任何两条曲线恰好相交于两点,任何三条曲线不相交于同一点,问这些曲线将平面分割成的区域个数。
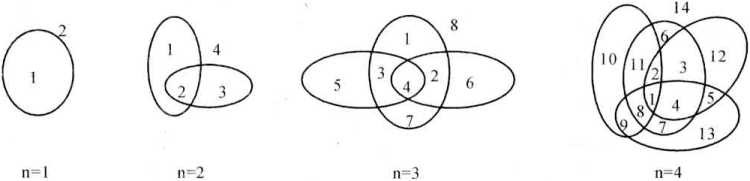
递推关系:
边界条件:
示例计算:
这种问题在竞赛中经常出现,考察理解几何图形的分割特性。
递推关系推导过程
平面分割问题涉及通过n条曲线将平面分割成若干区域。我们可以使用递推关系来解决这个问题。假设我们已经知道n-1条曲线将平面分割成的区域数,那么我们可以通过引入第n条曲线来推导出n条曲线分割平面的区域数。
基本情况(n=1):
- 一条曲线将平面分割成的区域数显然是2。
递推关系:
- 设
R(n)为 n 条曲线将平面分割成的区域数。 - 当有
n-1条曲线时,分割成的区域数为R(n-1)。 - 第 n 条曲线每与前面的每一条曲线恰好相交于2点,形成新的区域。
第 n 条曲线与每条已有曲线相交的两点将前面形成的区域再分成两部分。由于第 n 条曲线与之前的每条曲线相交两次,所以会产生新的区域。
- 设
推导递推公式:
- 引入第 n 条曲线,和之前的
n-1条曲线每条相交两次,总共产生2(n-1)个新的区域。 - 因此,新增的区域数是
2(n-1)。 - 所以,
R(n) = R(n-1) + 2(n-1)。
- 引入第 n 条曲线,和之前的
初始条件:
- 当 n = 1 时,
R(1) = 2。
- 当 n = 1 时,
综合起来,递推关系为:
R(n) = R(n-1) + 2(n-1)
小练习
问题:
编写一个C++程序,计算并输出n条封闭曲线将平面分割成的区域个数。
代码:
#include <iostream> // 包含输入输出流库
using namespace std; // 使用标准命名空间
int planeDivision(int n) { // 定义函数planeDivision,参数为n,用于计算平面划分的区域数
if (n == 1) return 2; // 如果输入为1,直接返回2
return planeDivision(n - 1) + 2 * (n - 1); // 递归调用planeDivision函数,计算n-1时的结果并加上当前层的区域数
}
int main() { // 主函数
int n; // 定义整型变量n,用于存储用户输入的闭合曲线数量
cout << "Enter the number of closed curves: "; // 输出提示信息,要求用户输入闭合曲线的数量
cin >> n; // 从标准输入流中读取用户输入的闭合曲线数量,并存储到变量n中
cout << "Number of regions: " << planeDivision(n) << endl; // 输出计算得到的平面划分区域数
return 0; // 返回0,表示程序执行成功
}
平面分割问题: 使用递归方法计算n条封闭曲线将平面分割成的区域个数。
# 4. Catalan 数
基本概念
Catalan数是一类在组合数学中出现的整数数列,以法国数学家Eugène Charles Catalan的名字命名。Catalan数通常用 Cn 表示,其定义如下:
在一个凸 n 边形中,通过不相交的对角线将其拆分成若干三角形,不同的拆分方案数目称为 n 的Catalan数,即 Cn。
Catalan数的前几个值是:
Catalan数在组合计数问题中具有广泛的应用,如:
- 括号匹配问题:用
n对括号能够组成多少种合法的括号序列。 - 凸多边形三角剖分问题:在一个
n边形中,通过不相交的对角线将其分割成多少个三角形。 - 凸多边形的顶点连线问题:在一个
n边形的顶点上连接线段,使得线段两两不相交,问有多少种方案。
Catalan数的计算可以通过递推关系或直接计算公式进行。
问题提出:
在一个凸n边形中,通过不相交的对角线将其拆分成若干三角形,不同的拆分方案数用 Cn 表示。
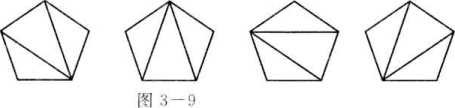
递推关系:
这个递推关系表示,第 n 个Catalan数等于前 n-1 个Catalan数的乘积之和。
边界条件为 C0=1,即空序列也算作一种括号匹配方案。
边界条件:
示例计算: 对于五边形:
Catalan数常用于组合计数问题,如计算不同的括号匹配方式。
小练习
问题:
编写一个C++程序,计算并输出一个凸n边形的三角拆分方案数。
代码:
#include <iostream> // 包含输入输出流头文件
using namespace std; // 使用标准命名空间
int catalan(int n) { // 定义函数 catalan,计算卡特兰数
if (n <= 1) return 1; // 若 n 小于等于 1,则返回 1,卡特兰数的基本情况
int res = 0; // 初始化结果为 0
for (int i = 1; i < n; ++i) // 循环遍历计算 catalan(n) 的递归公式
res += catalan(i) * catalan(n - i); // 使用卡特兰数的递归公式计算结果
return res; // 返回计算得到的结果
}
int main() { // 主函数
int n; // 定义整数变量 n,表示多边形的边数
cout << "Enter the number of sides in the polygon: "; // 提示用户输入多边形的边数
cin >> n; // 读取用户输入的边数
cout << "Number of triangulation schemes: " << catalan(n - 1) << endl; // 输出多边形的三角剖分方案数
return 0; // 返回执行成功的状态码
}
Catalan 数: 使用递归方法计算一个凸n边形的三角拆分方案数。
# 5. 第二类 Stirling 数
基本概念
第二类 Stirling 数是组合数学中的一类重要数列,通常用 S(n, m) 表示。它描述的是将n个有区别的物体分成m个非空的不可区分的集合(盒子)的不同方案数。
具体地,第二类 Stirling 数 S(n, m) 表示将n个有区别的物体分成m个非空的不可区分的集合的方案数。换句话说,它表示的是将n个物体放入m个盒子中,且每个盒子至少有一个物体的方案数。
第二类 Stirling 数的递推关系如下:
其中边界条件为:
第二类 Stirling 数在组合计数问题中有广泛的应用,例如将物体划分成不同的集合,或者将物体放入盒子中等问题。
定义:
n个有区别的球放入m个相同的盒子中,要求无一空盒,其不同的方案数用 S(n, m) 表示。
递推关系:
边界条件:
也就是,对于S(n, m)来说
- 当
m = 0时,S(n, m) = 0或 - 当
m = 1时,S(n, m) = 1或 - 当
m = n时,S(n, m) = 1或 - 当
n < m时,S(n, m) = 0
示例计算:
第二类Stirling数用于解决组合分割问题。
递推关系推导过程
第二类 Stirling 数 S(n, m) 表示将 n 个不同的元素分配到 m 个非空集合的方式数。它的递推关系是:
S(n, m) = m * S(n-1, m) + S(n-1, m-1)
以下是这个递推关系的推导过程:
递推关系的基本思想:
将
n个不同的元素分配到m个非空集合,我们可以考虑第n个元素的情况:情况 1:第
n个元素独自成一个新集合,那么剩下的n-1个元素需要分配到剩下的m-1个非空集合中。此时的方案数是S(n-1, m-1)。情况 2:第
n个元素不独自成一个新集合,而是加入到现有的m个集合中的一个。此时我们有m个选择让第n个元素加入。因此,剩下的n-1个元素分配到m个非空集合的方案数是S(n-1, m),且我们有m个集合可以选择加入第n个元素。
将这两种情况综合:
将上述两种情况的方案数相加:
S(n, m) = S(n-1, m-1) + m * S(n-1, m)边界条件:
边界条件主要有以下几个:
S(0, 0) = 1,表示将 0 个元素分配到 0 个集合的方式只有一种,即什么都不做。S(n, 0) = 0对于n > 0,表示不能将n个元素分配到 0 个集合中。S(0, m) = 0对于m > 0,表示不能将 0 个元素分配到非 0 个集合中。S(n, m) = 0对于n < m,表示不能将n个元素分配到比n更多的非空集合中。S(n, n) = 1,表示将n个元素分配到n个集合的方式只有一种,即每个集合中正好一个元素。
综上所述,第二类 Stirling 数 S(n, m) 的递推关系为:
S(n, m) = m * S(n-1, m) + S(n-1, m-1)
并且具有以下边界条件:
S(0, 0) = 1, S(n, 0) = 0 对于 n > 0, S(0, m) = 0 对于 m > 0, S(n, m) = 0 对于 n < m, S(n, n) = 1
小练习
问题:
编写一个C++程序,计算并输出将n个不同的球放入m个相同的盒子中且无空盒的不同方案数。
代码:
#include <iostream> // 包含输入输出流库
using namespace std; // 使用标准命名空间
int stirling(int n, int m) { // 定义斯特林数函数,参数为n和m
if (n == 0 || m == 0 || m > n) return 0; // 如果n为0或者m为0或者m大于n,则返回0
if (m == 1 || m == n) return 1; // 如果m为1或者m等于n,则返回1
return m * stirling(n - 1, m) + stirling(n - 1, m - 1); // 递归计算斯特林数
}
int main() { // 主函数
int n, m; // 声明整型变量n和m
cout << "Enter the number of balls: "; // 输出提示信息,要求输入球的数量
cin >> n; // 从标准输入获取球的数量
cout << "Enter the number of boxes: "; // 输出提示信息,要求输入箱子的数量
cin >> m; // 从标准输入获取箱子的数量
cout << "Number of ways to distribute the balls: " << stirling(n, m) << endl; // 输出分配球的方法数
return 0; // 返回0表示程序正常结束
}
第二类 Stirling 数: 使用递归方法计算将n个不同的球放入m个相同的盒子中且无空盒的不同方案数。