图
# 图的基本概念
**图(Graph)是一种非线性数据结构,由顶点(vertex)和边(edge)**组成。图 可以抽象地表示为顶点集合 和边集合 的组合。通常情况下,图的数据结构会表示为 。
示例:一个包含 5 个顶点和 7 条边的图。
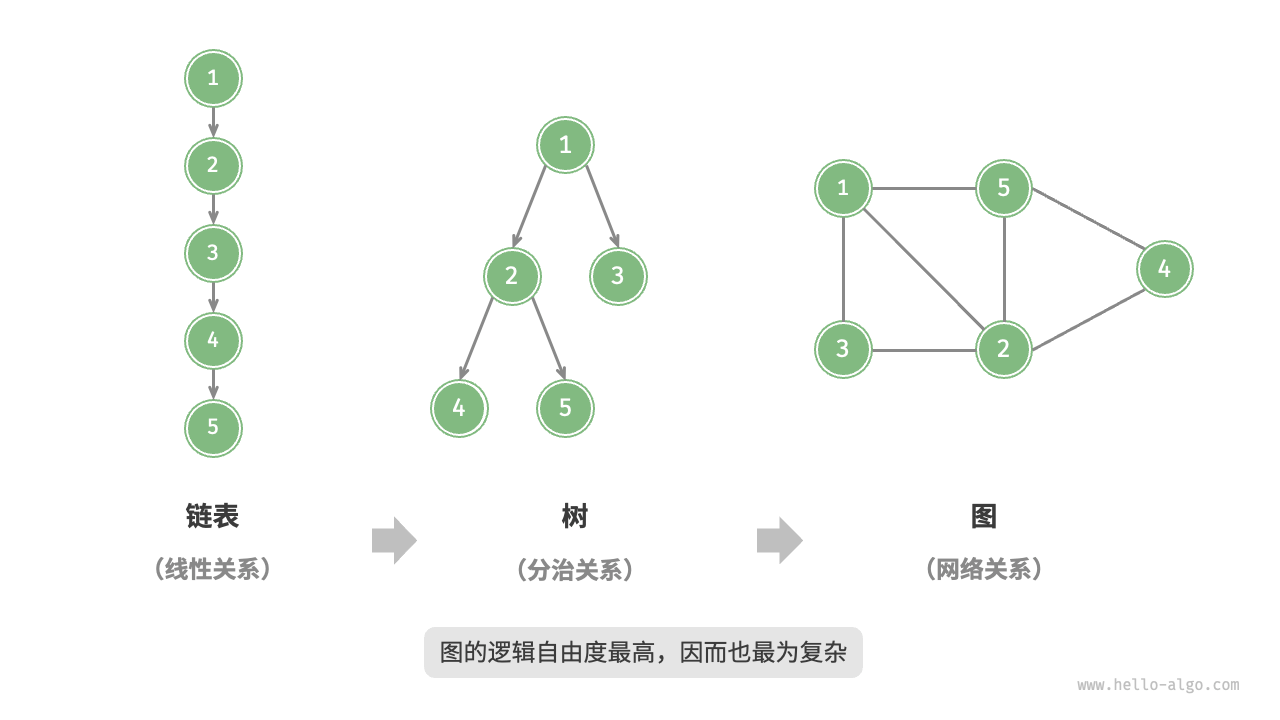
在图数据结构中,顶点可以看作节点,边则是连接这些节点的引用(指针)。图是一种从链表和树数据结构扩展而来的更复杂的结构。
图、链表、树之间的关系如图 1 所示:
- 链表:线性结构。
- 树:分层结构。
- 图:网络结构,拥有更高的自由度和复杂性。
# 图的类型与术语
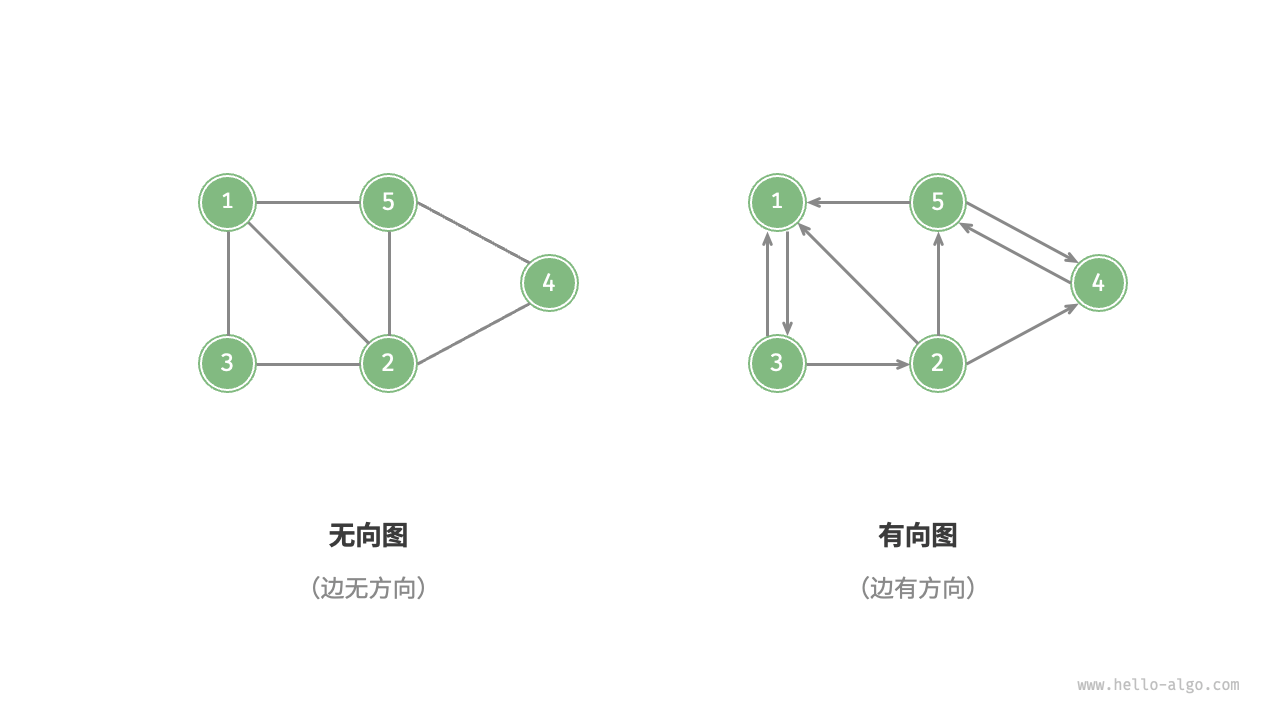
# 1. 按边的方向性分类
- 无向图(Undirected Graph):边表示顶点之间的“双向”连接。比如社交媒体中的好友关系。
- 有向图(Directed Graph):边具有方向性, 和 表示两个独立的方向。比如社交媒体中的关注与被关注关系。
有向图与无向图如图 2 所示。
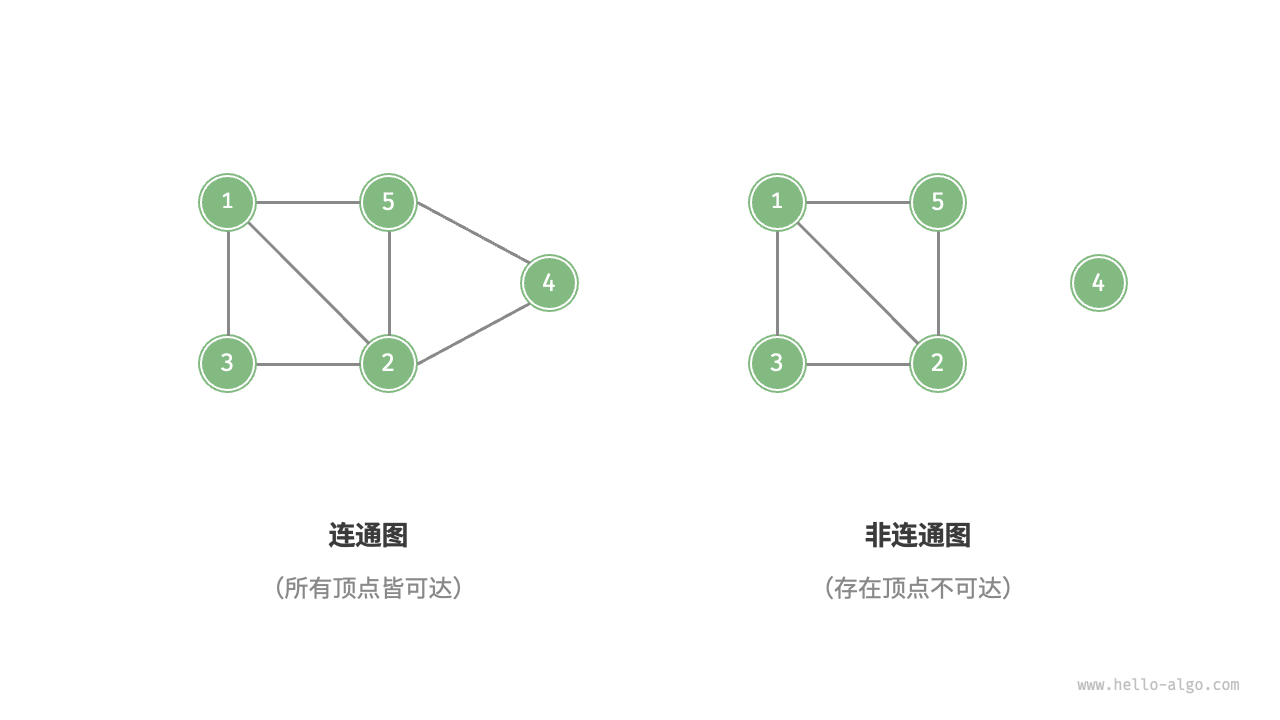
# 2. 按顶点的连通性分类
- 连通图(Connected Graph):从某个顶点出发可以到达其他所有顶点。
- 非连通图(Disconnected Graph):存在至少一个顶点无法从其他顶点到达。
连通图与非连通图如图 3 所示。
# 3. 按边的权重分类
- 有权图(Weighted Graph):边带有权重,表示不同的关系强度或距离。比如在游戏中的玩家亲密度。
- 无权图(Unweighted Graph):边不带权重。
有权图与无权图如图 4 所示。
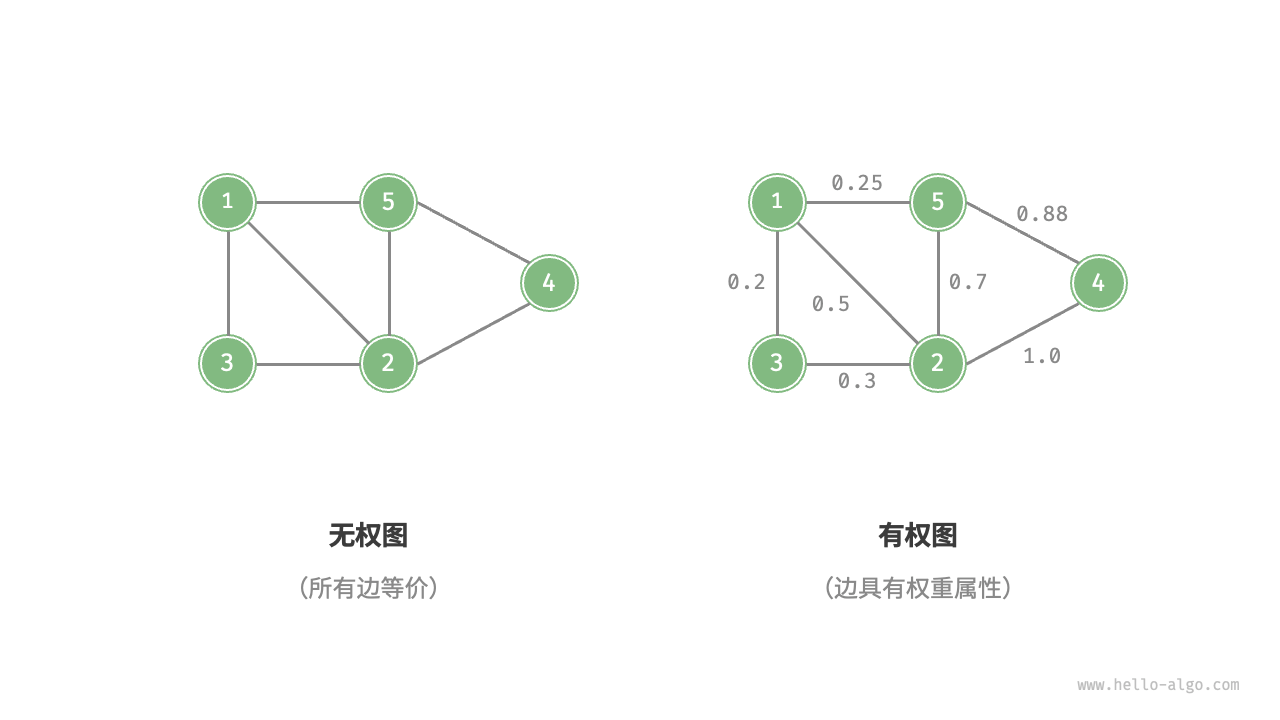
# 常用术语
- 邻接(Adjacency):两个顶点之间有边相连时,称这两个顶点为邻接。在图 4 中,顶点 1 的邻接顶点为 2、3、5。
- 路径(Path):从顶点 A 到顶点 B 经过的边序列。例如在图 4 中,边序列 1-5-2-4 是从顶点 1 到顶点 4 的一条路径。
- 度(Degree):顶点拥有的边数。在有向图中,**入度(In-Degree)**表示指向该顶点的边数,**出度(Out-Degree)**表示从该顶点出发的边数。
# 图的表示方法
# 1. 邻接矩阵(Adjacency Matrix)
邻接矩阵使用一个 的矩阵表示图,其中 是顶点数量。矩阵的行和列对应于顶点,矩阵元素表示顶点之间的边,用 1 表示有边,0 表示无边。
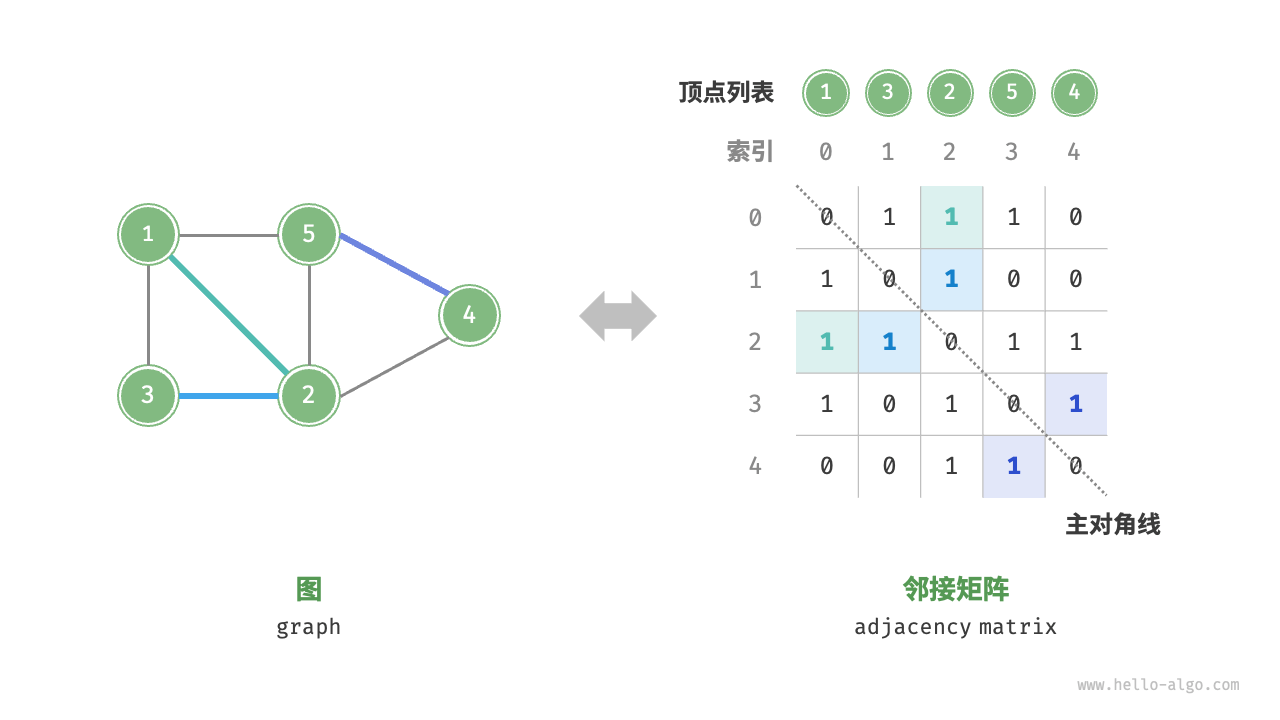
邻接矩阵的特性:
- 顶点不能与自身相连,因此主对角线元素没有意义。
- 对于无向图,矩阵关于主对角线对称。
- 可以通过将矩阵元素替换为权重表示有权图。
邻接矩阵适合快速访问边(时间复杂度 ),但空间复杂度为 ,内存占用较多。
# 2. 邻接表(Adjacency List)
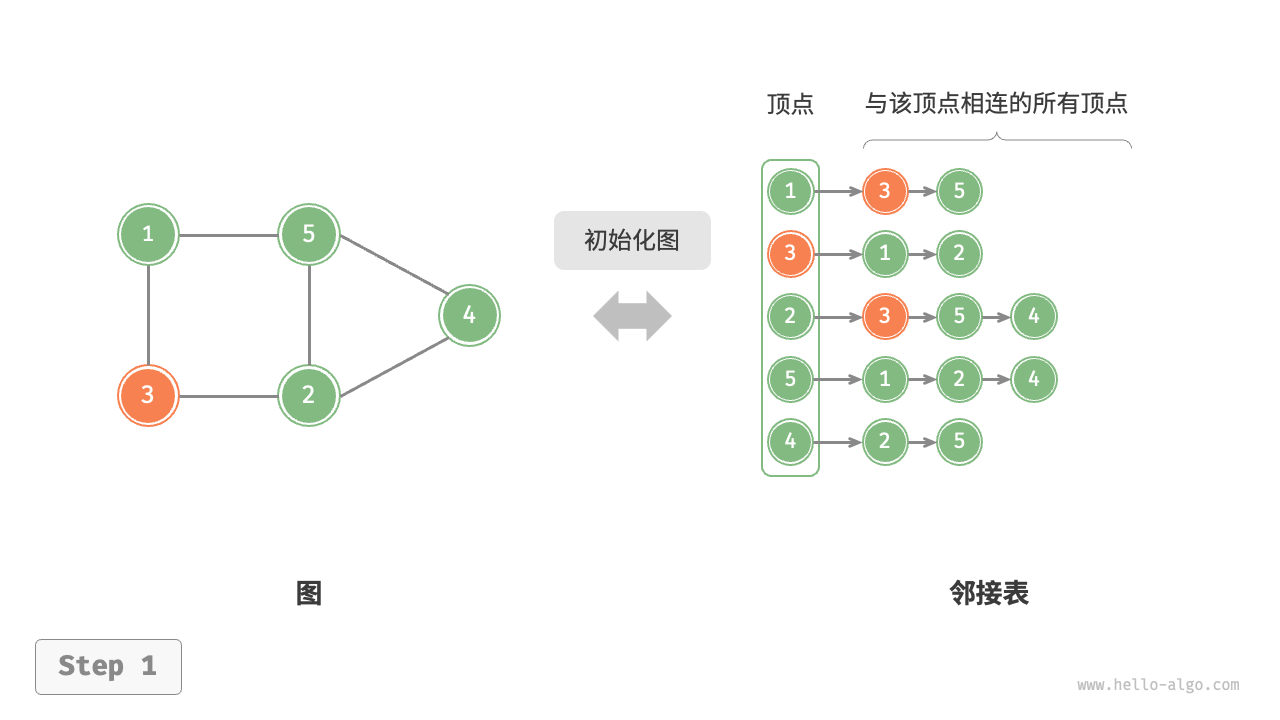
邻接表使用多个链表表示图,每个链表对应一个顶点,链表中的节点表示与该顶点相连的其他顶点。
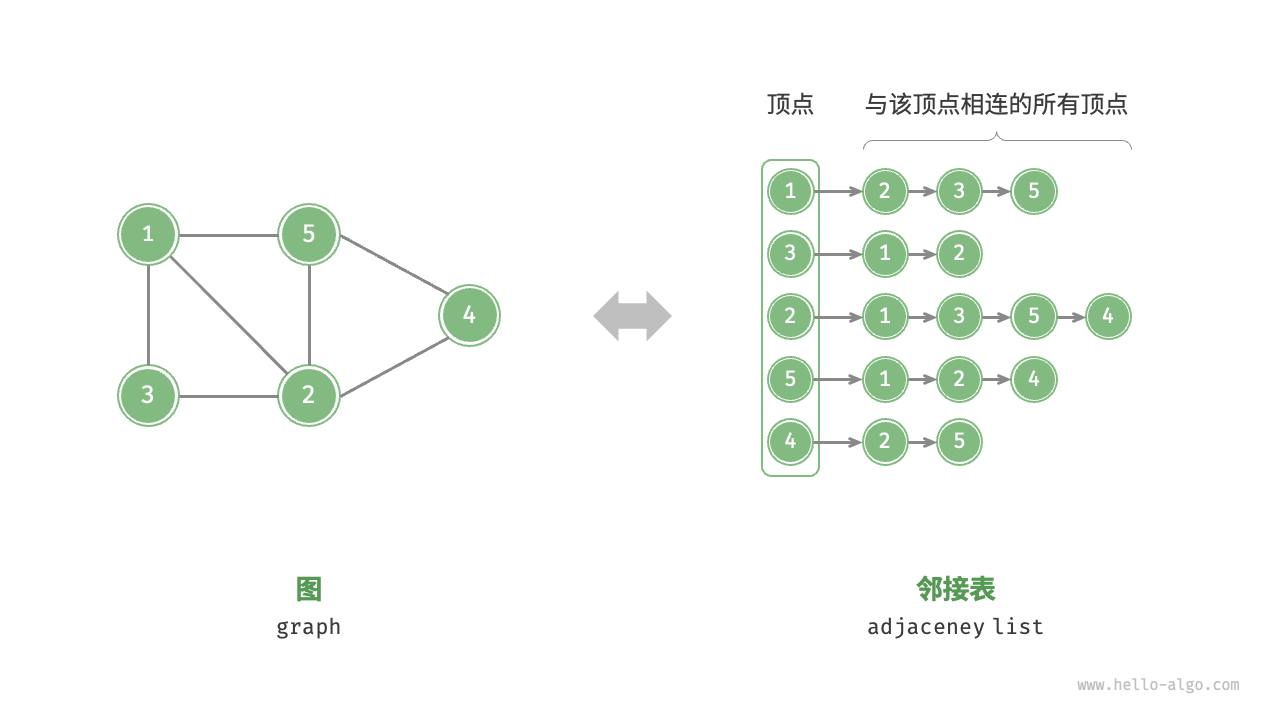
邻接表的特点:
- 只存储实际存在的边,适合稀疏图(边的数量远小于 )。
- 查找边的时间复杂度为 ,可以通过数据结构优化提高效率(如 AVL 树、红黑树、哈希表等)。
# 图的常见应用
图广泛应用于建模各种现实系统,以下是常见的图应用及对应的计算问题:
| 现实系统 | 顶点 | 边 | 图计算问题 |
|---|---|---|---|
| 社交网络 | 用户 | 好友关系 | 潜在好友推荐 |
| 地铁线路 | 站点 | 站点间的连通性 | 最短路线推荐 |
| 太阳系 | 星体 | 星体间的万有引力 | 行星轨道计算 |
# 图的基础操作
图的基础操作可分为对“边”的操作和对“顶点”的操作。在“邻接矩阵”和“邻接表”两种表示方法下,实现方式有所不同。
# 基于邻接矩阵的实现
给定一个顶点数量为 的无向图,则各种操作的实现方式如下图所示。
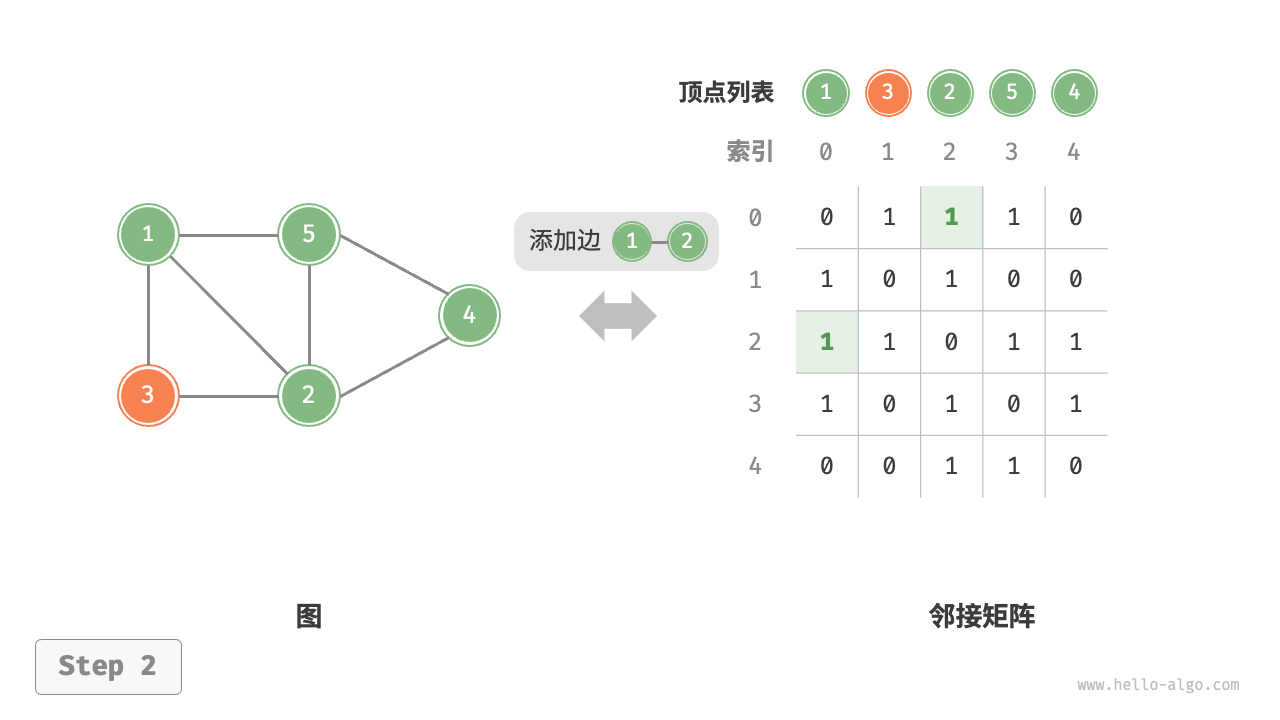
- 添加或删除边:直接在邻接矩阵中修改指定的边即可,使用 时间。而由于是无向图,因此需要同时更新两个方向的边。
- 添加顶点:在邻接矩阵的尾部添加一行一列,并全部填 即可,使用 时间。
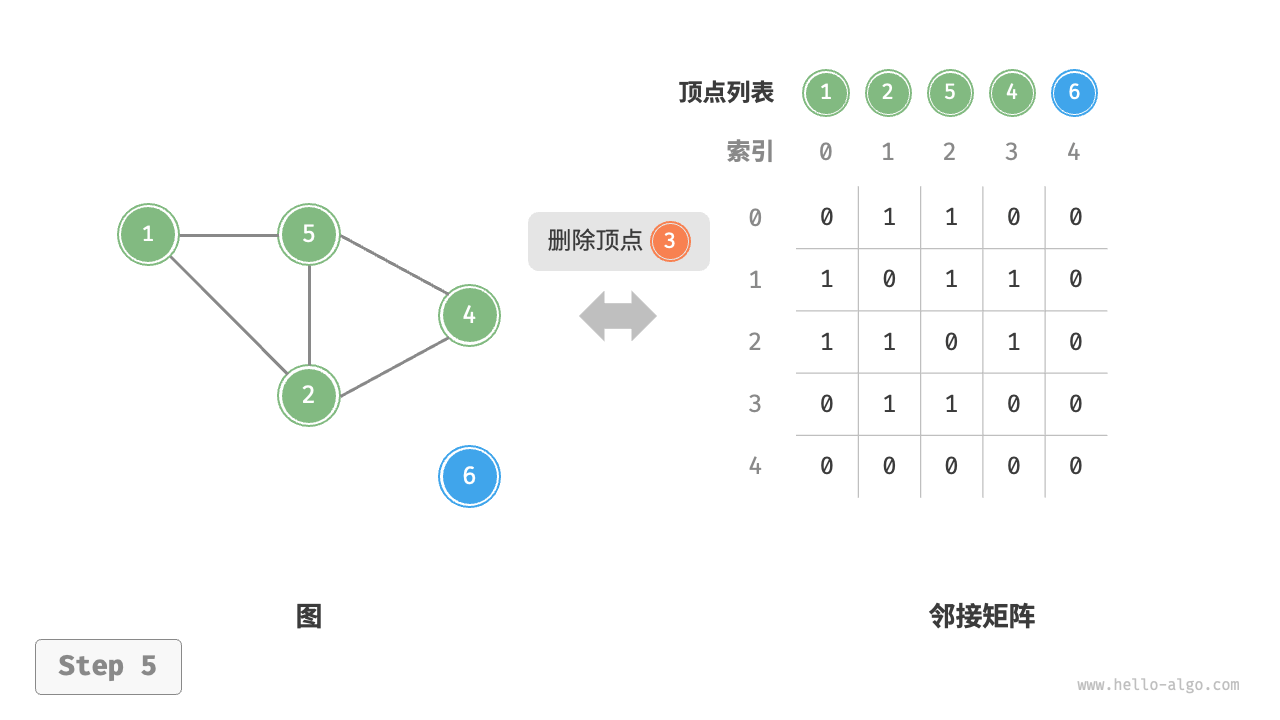
- 删除顶点:在邻接矩阵中删除一行一列。当删除首行首列时达到最差情况,需要将 个元素“向左上移动”,从而使用 时间。
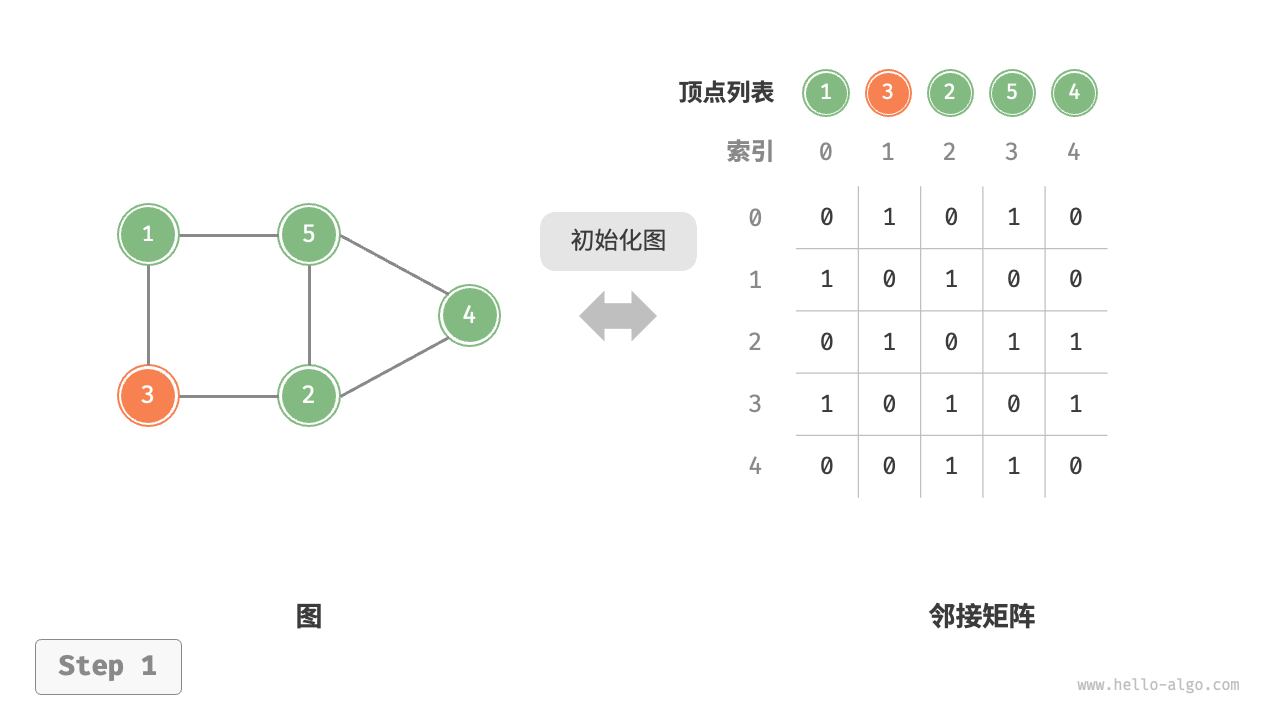
- 初始化:传入 个顶点,初始化长度为 的顶点列表
vertices,使用 时间;初始化 大小的邻接矩阵adjMat,使用 时间。
"初始化邻接矩阵"
"添加边"
"删除边"
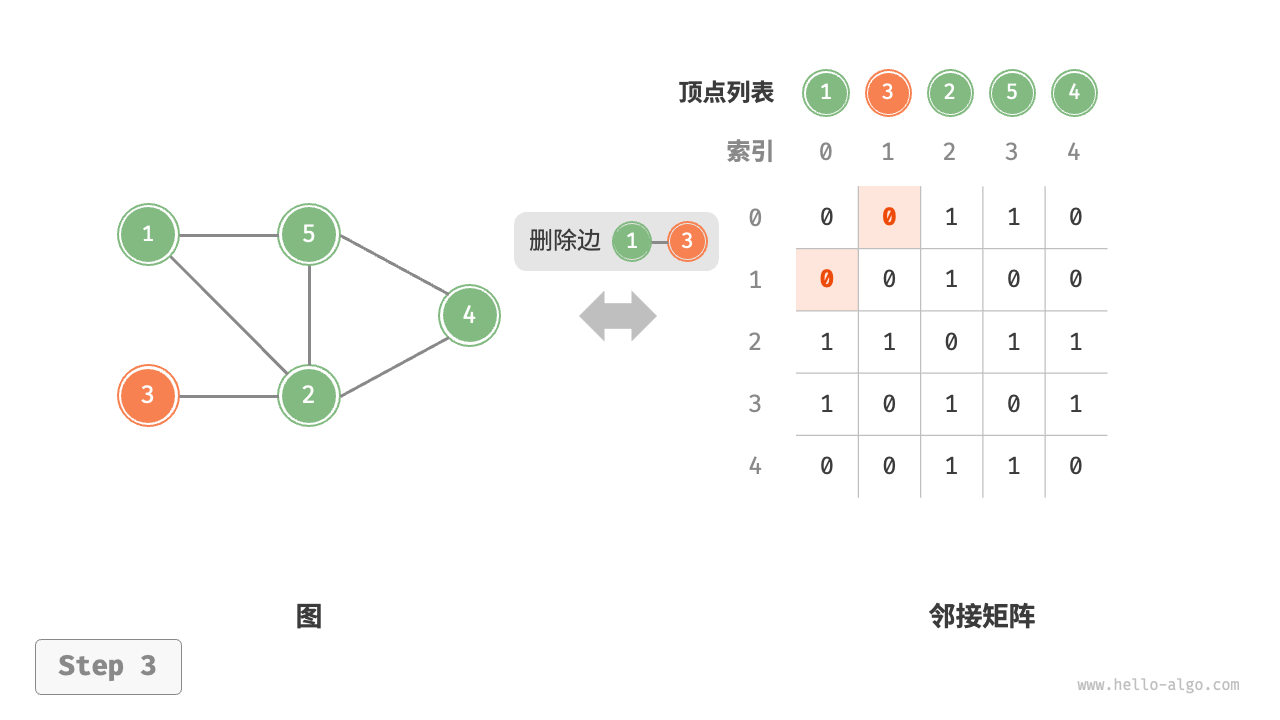
"添加顶点"
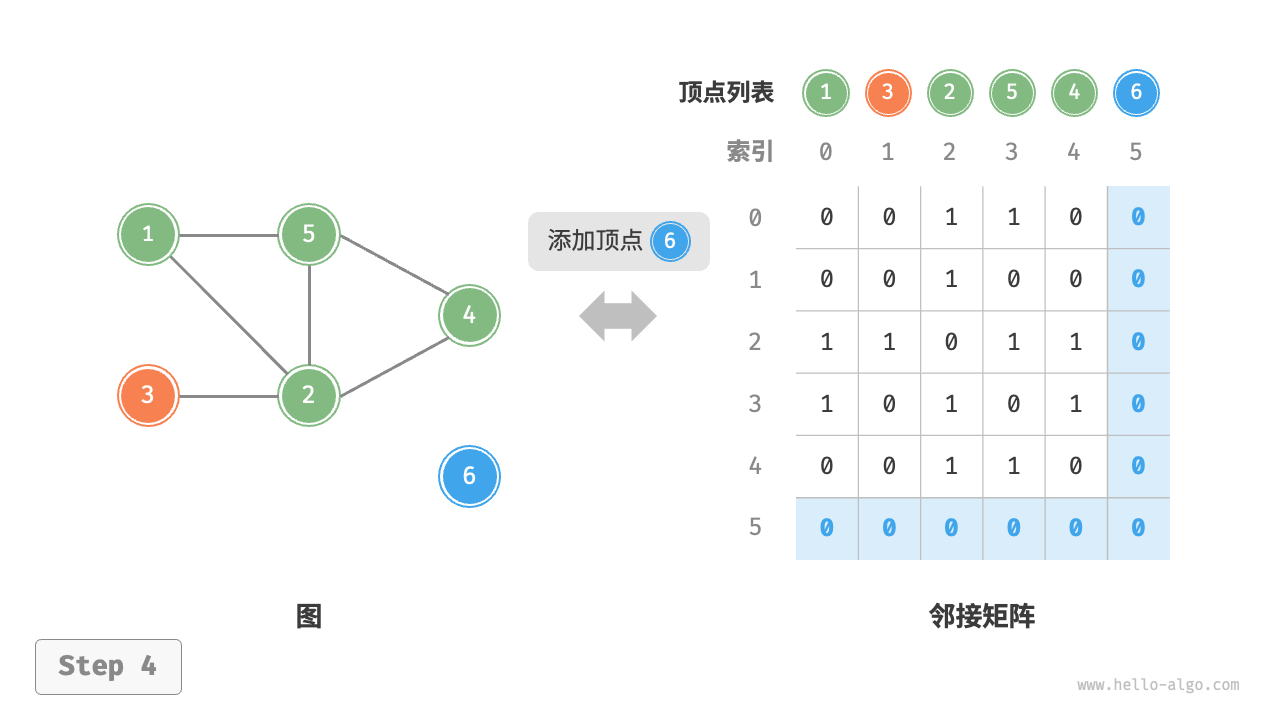
"删除顶点"
# 基于邻接表的实现
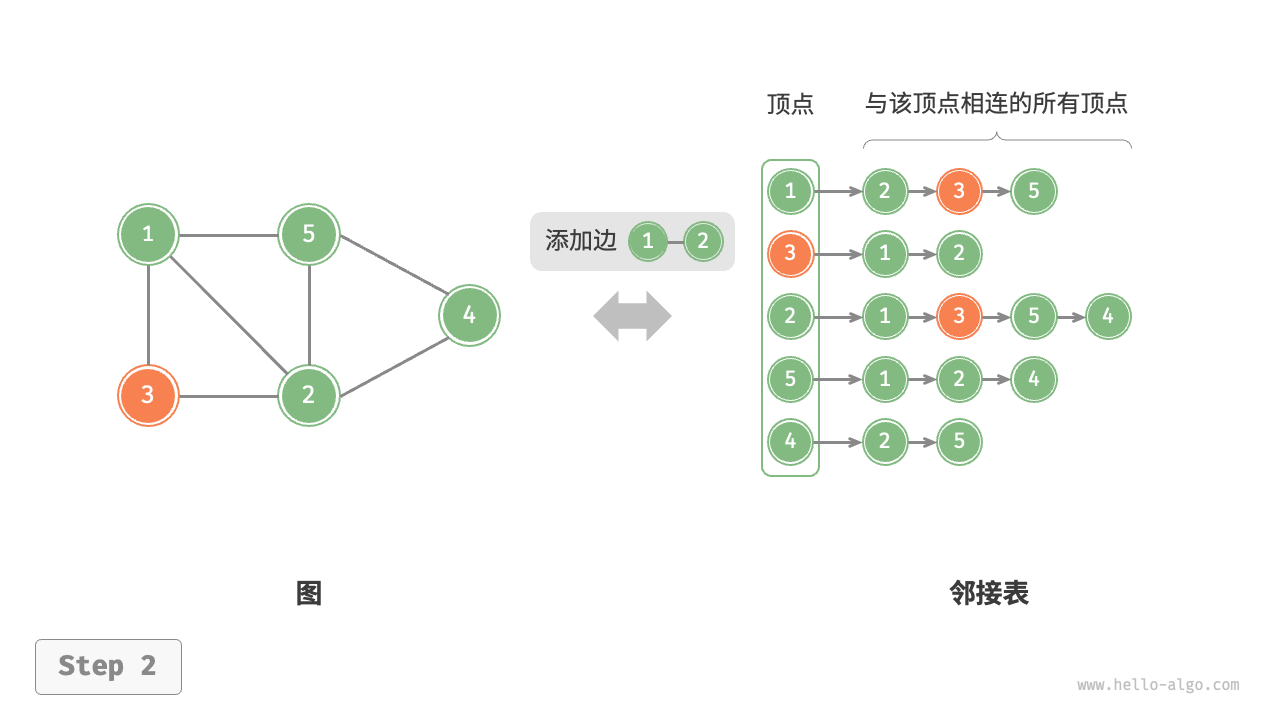
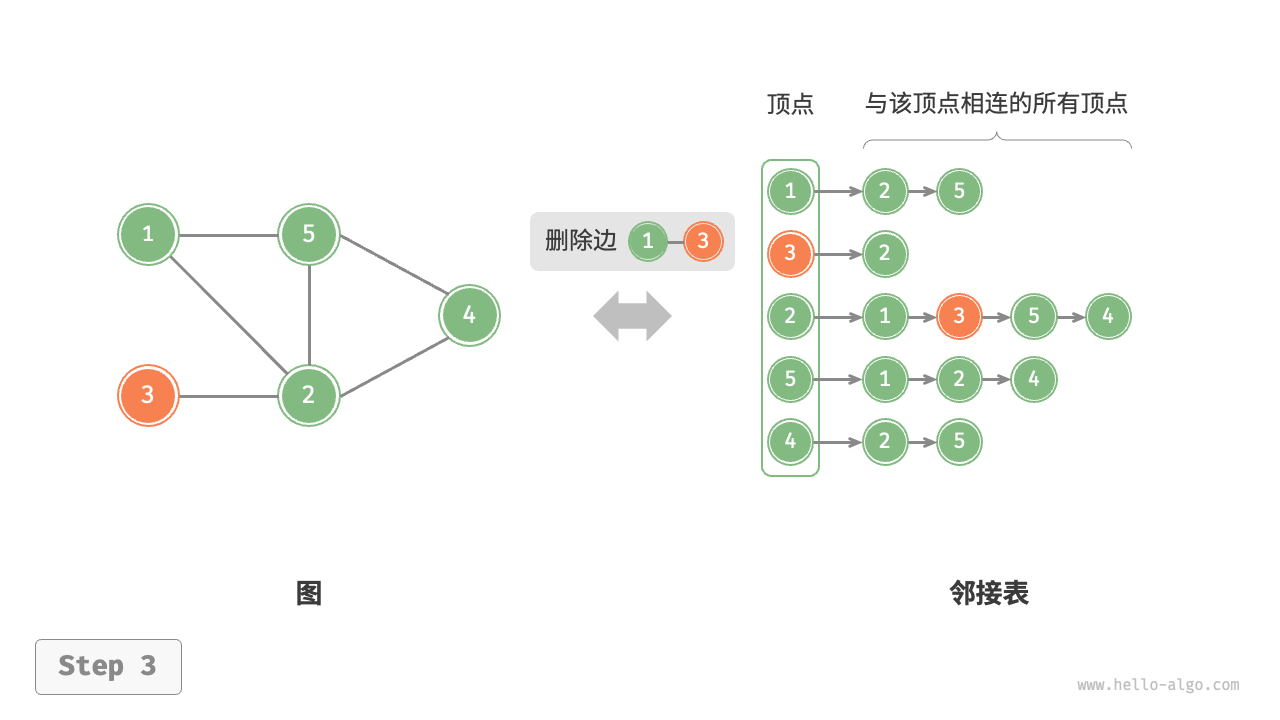
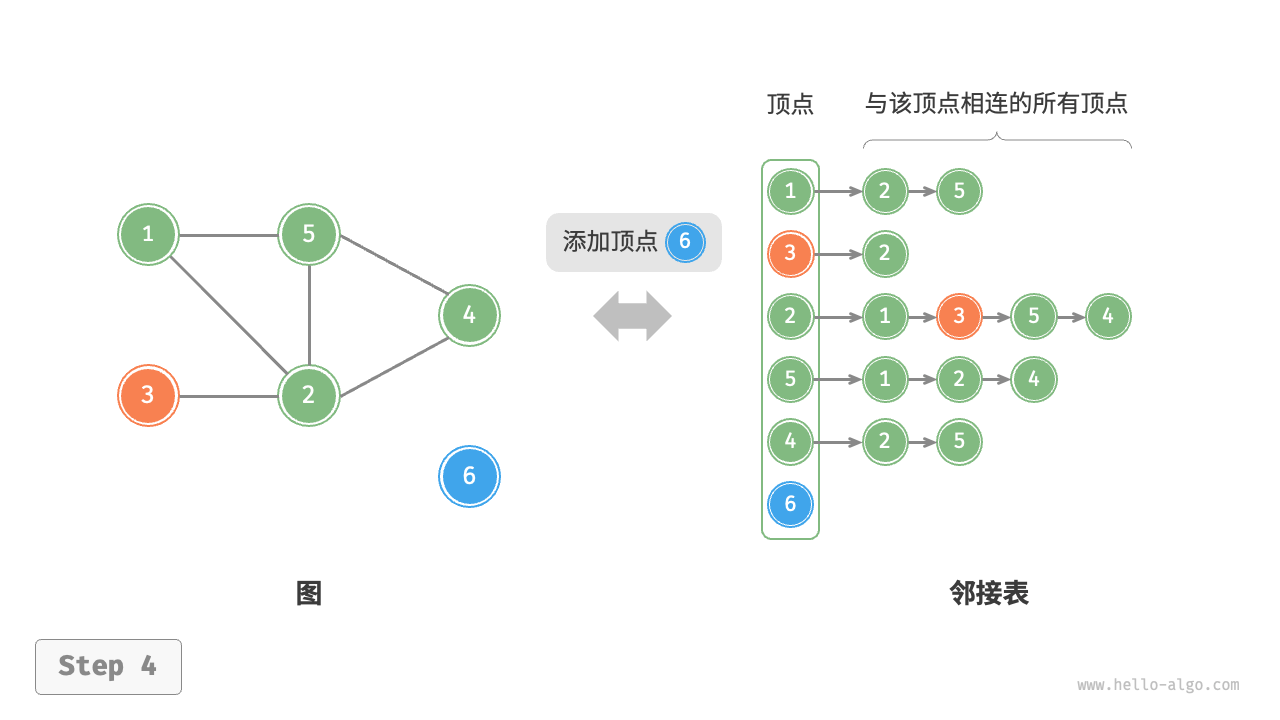
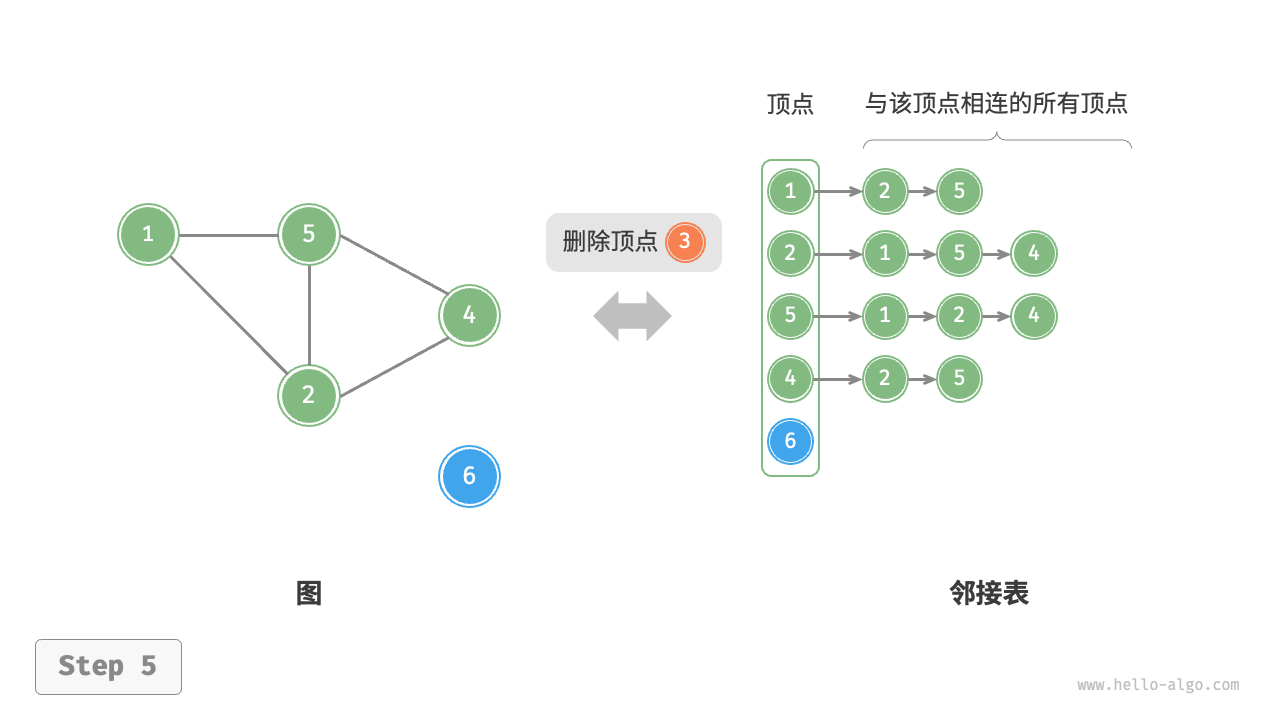
设无向图的顶点总数为 、边总数为 ,则可根据下图所示的方法实现各种操作。
- 添加边:在顶点对应链表的末尾添加边即可,使用 时间。因为是无向图,所以需要同时添加两个方向的边。
- 删除边:在顶点对应链表中查找并删除指定边,使用 时间。在无向图中,需要同时删除两个方向的边。
- 添加顶点:在邻接表中添加一个链表,并将新增顶点作为链表头节点,使用 时间。
- 删除顶点:需遍历整个邻接表,删除包含指定顶点的所有边,使用 时间。
- 初始化:在邻接表中创建 个顶点和 条边,使用 时间。
"初始化邻接表"
"添加边"
"删除边"
"添加顶点"
"删除顶点"
# 效率对比
设图中共有 个顶点和 条边,下表对比了邻接矩阵和邻接表的时间效率和空间效率。
表 邻接矩阵与邻接表对比
| 邻接矩阵 | 邻接表(链表) | 邻接表(哈希表) | |
|---|---|---|---|
| 判断是否邻接 | |||
| 添加边 | |||
| 删除边 | |||
| 添加顶点 | |||
| 删除顶点 | |||
| 内存空间占用 |
观察上表,似乎邻接表(哈希表)的时间效率与空间效率最优。但实际上,在邻接矩阵中操作边的效率更高,只需一次数组访问或赋值操作即可。综合来看,邻接矩阵体现了“以空间换时间”的原则,而邻接表体现了“以时间换空间”的原则。
# 图的遍历
树代表的是“一对多”的关系,而图则具有更高的自由度,可以表示任意的“多对多”关系。因此,我们可以把树看作图的一种特例。显然,树的遍历操作也是图的遍历操作的一种特例。
图和树都需要应用搜索算法来实现遍历操作。图的遍历方式也可分为两种:广度优先遍历和深度优先遍历。
# 广度优先遍历
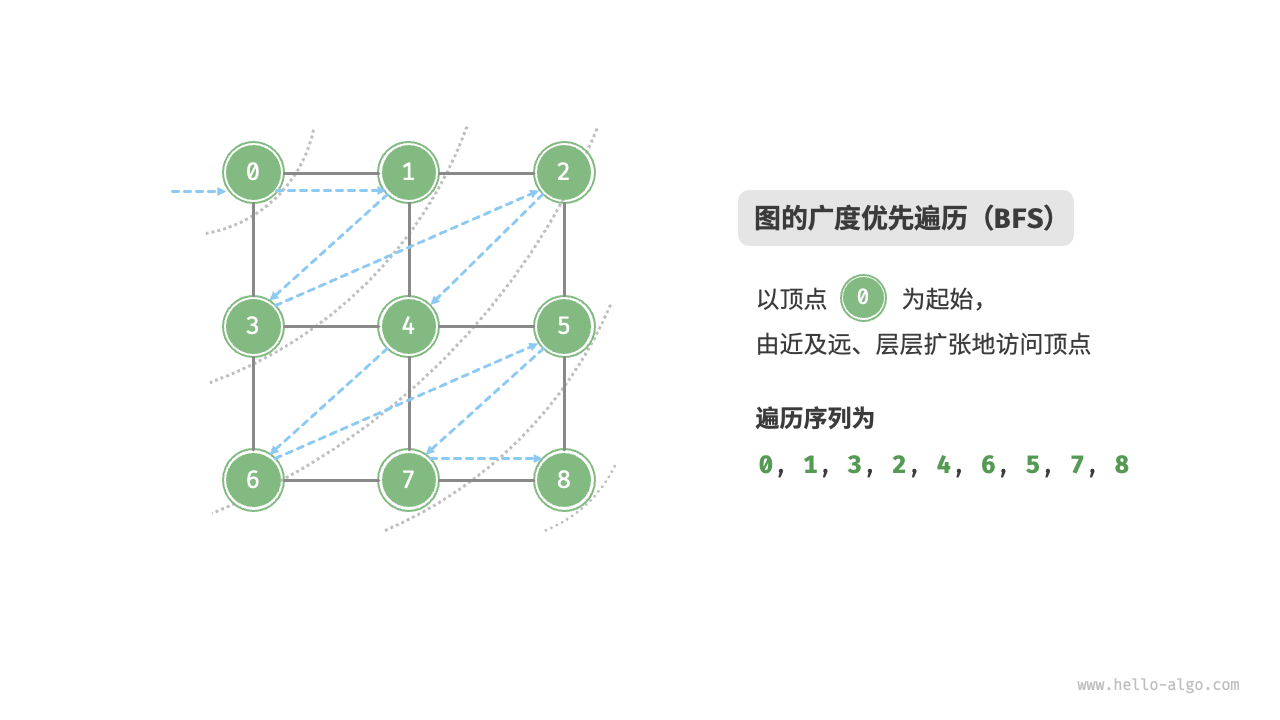
广度优先遍历是一种由近及远的遍历方式,从某个节点出发,始终优先访问距离最近的顶点,并一层层向外扩张。如下图所示,从左上角顶点出发,首先遍历该顶点的所有邻接顶点,然后遍历下一个顶点的所有邻接顶点,以此类推,直至所有顶点访问完毕。
# 算法实现
BFS 通常借助队列来实现,代码如下所示。队列具有“先入先出”的性质,这与 BFS 的“由近及远”的思想异曲同工。
- 将遍历起始顶点
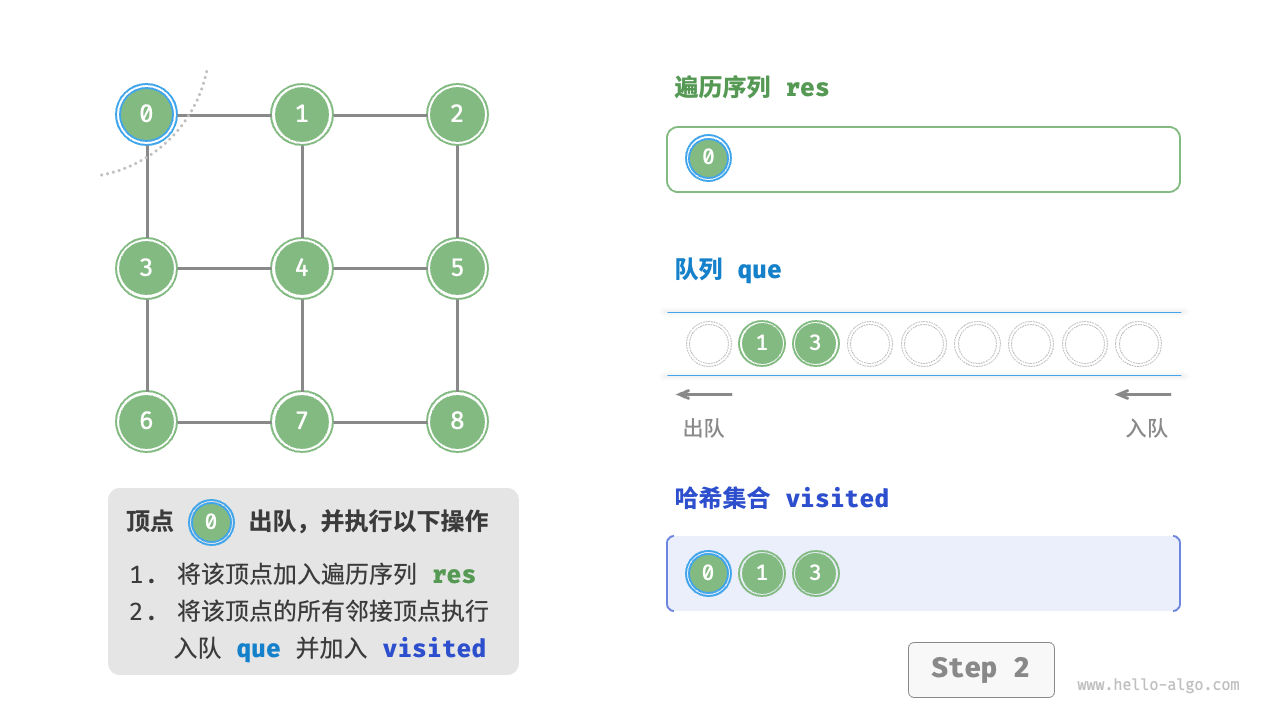
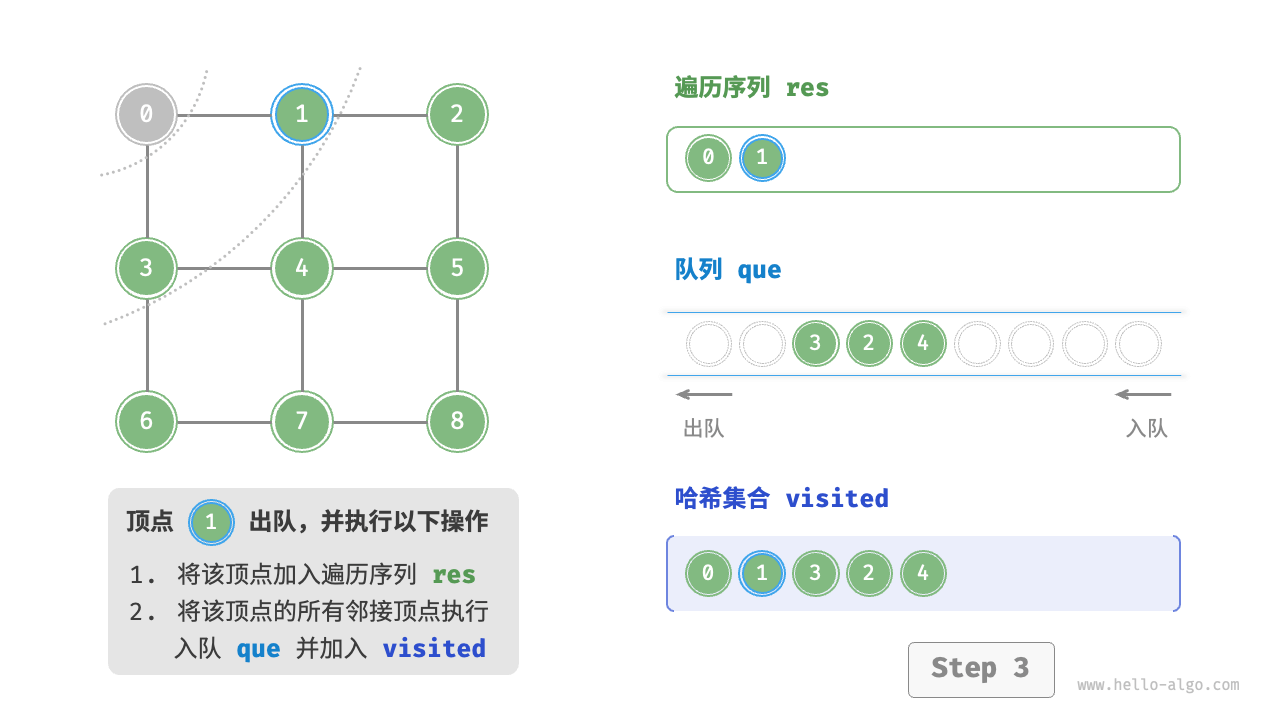
startVet加入队列,并开启循环。 - 在循环的每轮迭代中,弹出队首顶点并记录访问,然后将该顶点的所有邻接顶点加入到队列尾部。
- 循环步骤
2.,直到所有顶点被访问完毕后结束。
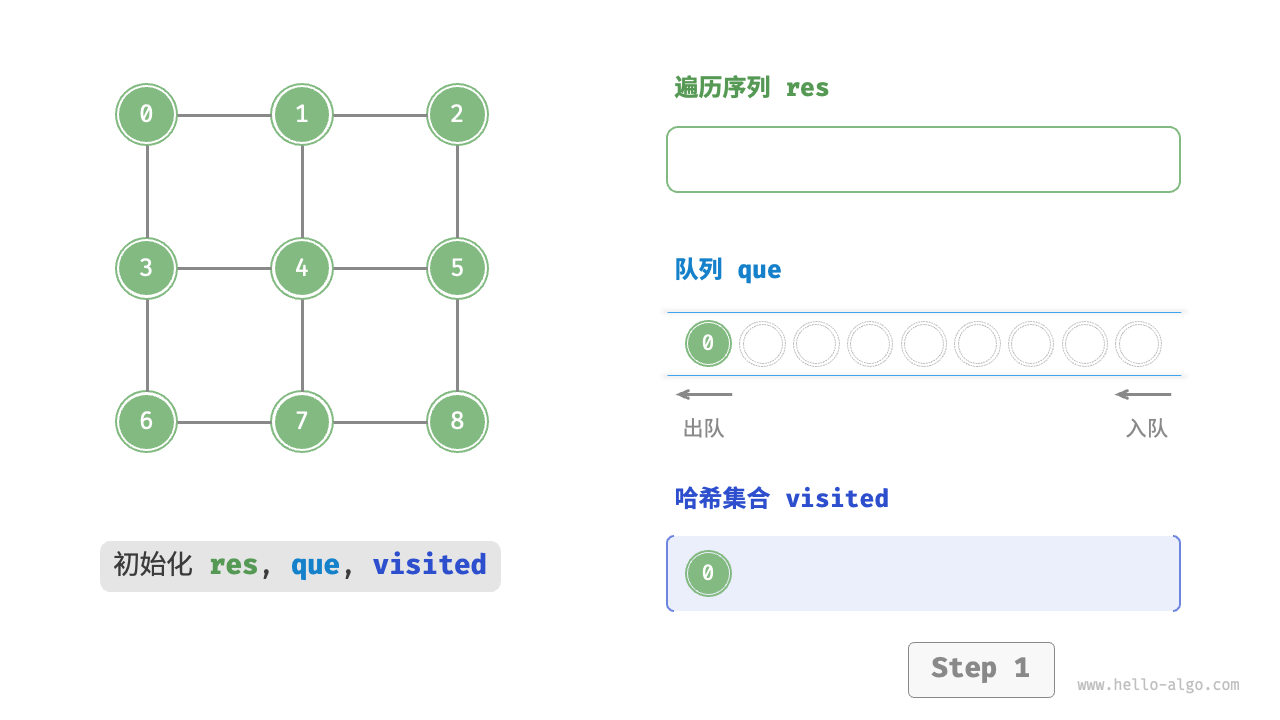
为了防止重复遍历顶点,我们需要借助一个哈希集合 visited 来记录哪些节点已被访问。
哈希集合可以看作一个只存储
key而不存储value的哈希表,它可以在 时间复杂度下进行key的增删查改操作。根据key的唯一性,哈希集合通常用于数据去重等场景。
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_set> // 哈希集合
using namespace std;
// 结构体表示图的顶点
struct Vertex {
vector<int> neighbors; // 邻接顶点
};
int main() {
// 创建一个包含 6 个顶点的图
int numVertices = 6;
vector<Vertex> graph(numVertices);
// 添加边 (无向图)
graph[0].neighbors.push_back(1);
graph[0].neighbors.push_back(2);
graph[1].neighbors.push_back(0);
graph[1].neighbors.push_back(3);
graph[2].neighbors.push_back(0);
graph[2].neighbors.push_back(3);
graph[3].neighbors.push_back(1);
graph[3].neighbors.push_back(2);
graph[3].neighbors.push_back(4);
graph[4].neighbors.push_back(3);
graph[4].neighbors.push_back(5);
graph[5].neighbors.push_back(4);
// 广度优先遍历 (从顶点 0 开始)
queue<int> q;
unordered_set<int> visited;
// 将起始顶点加入队列并标记为已访问
q.push(0);
visited.insert(0);
cout << "广度优先遍历的顺序如下:" << endl;
while (!q.empty()) {
// 弹出队首顶点并访问
int currentVertex = q.front();
q.pop();
cout << "访问顶点: " << currentVertex << endl;
// 将所有未访问的邻接顶点加入队列
for (int neighbor : graph[currentVertex].neighbors) {
if (visited.find(neighbor) == visited.end()) {
q.push(neighbor);
visited.insert(neighbor);
}
}
}
return 0;
}
# 代码解析:
- 结构体
Vertex:用于存储每个顶点的邻接顶点列表(使用vector<int>)。 - 邻接表:使用
vector<Vertex>存储图的所有顶点,其中每个Vertex的neighbors保存与该顶点直接相连的其他顶点。 - 手动添加边:直接操作
graph数组来添加边。 - BFS 实现:与之前的类版本类似,通过队列和哈希集合来实现广度优先搜索,遍历从顶点
0开始。
在广度优先遍历 (BFS) 中,unordered_set 的作用是记录已经访问过的顶点,以避免重复访问同一个顶点。因为在图中,可能存在环或多个顶点指向同一个顶点。如果不进行标记,BFS 可能会陷入无限循环,或者多次访问同一个顶点,导致错误的遍历顺序。
- 举例说明: 假设有以下无向图:
0
/ \
1---2
\ /
3
从顶点 0 开始遍历,若没有记录已访问的顶点,BFS 将会如下操作:
- 从
0开始访问,将0的邻接顶点1和2加入队列。 - 访问
1,然后将1的邻接顶点0和3加入队列。注意,0已经被访问过,但此时它会被再次加入队列。 - 访问
2,将2的邻接顶点0和3加入队列。同样,0和3可能会被重复访问。 - 由于没有标记顶点已经访问过,遍历会继续处理这些重复的顶点,导致 BFS 不能正确结束或产生错误的遍历顺序。
因此,为了防止这种情况,需要一个数据结构来记录哪些顶点已经被访问过。unordered_set 由于其查找、插入的时间复杂度是 ,是非常合适的选择。每次访问一个顶点后,将该顶点加入 unordered_set,之后如果遇到已经存在于 unordered_set 中的顶点,就不再进行访问和处理。
- 示例解释:
unordered_set<int> visited;
visited是一个哈希集合,用来存储已经访问过的顶点。- 在访问一个顶点后,将其加入
visited:visited.insert(currentVertex); - 在访问邻接顶点之前,检查它是否已经被访问过:这里
if (visited.find(neighbor) == visited.end()) { q.push(neighbor); visited.insert(neighbor); }visited.find(neighbor)的返回值表示是否找到该顶点,如果没有找到,就将其加入队列,并标记为已访问。
这样,就可以防止 BFS 重复访问已经访问过的顶点,保证算法的正确性和效率。
图的广度优先遍历步骤
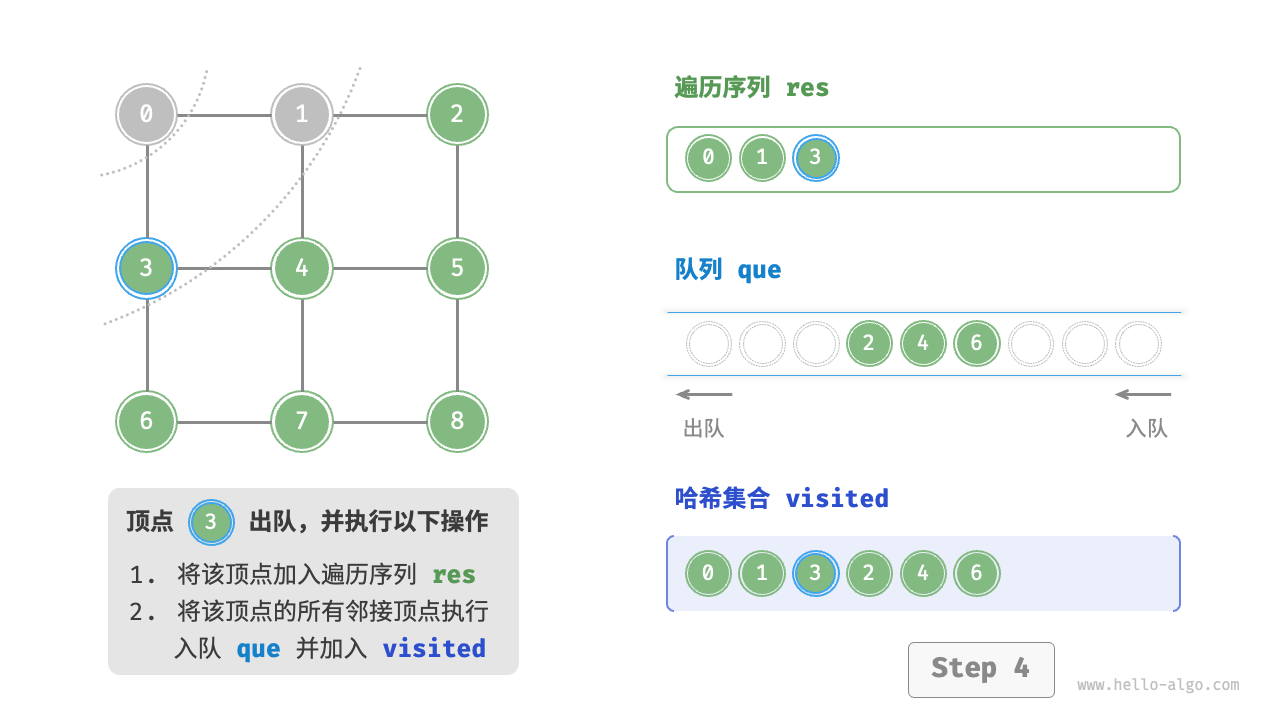
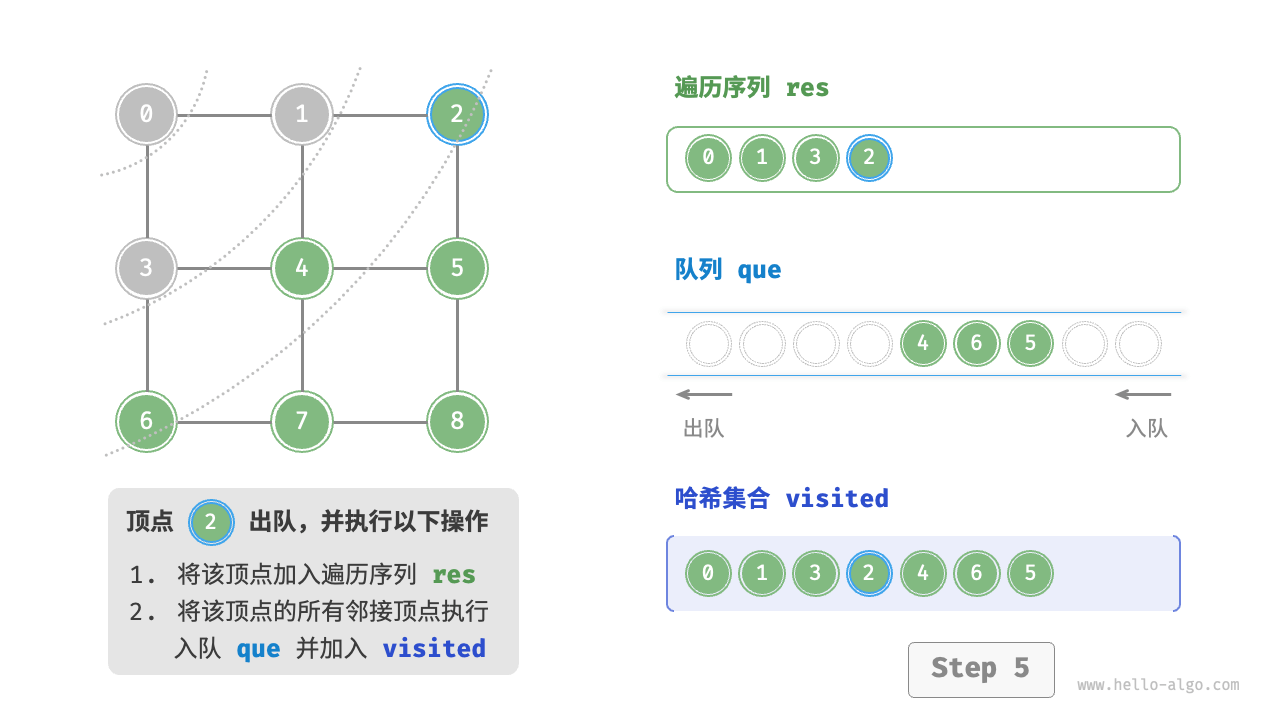
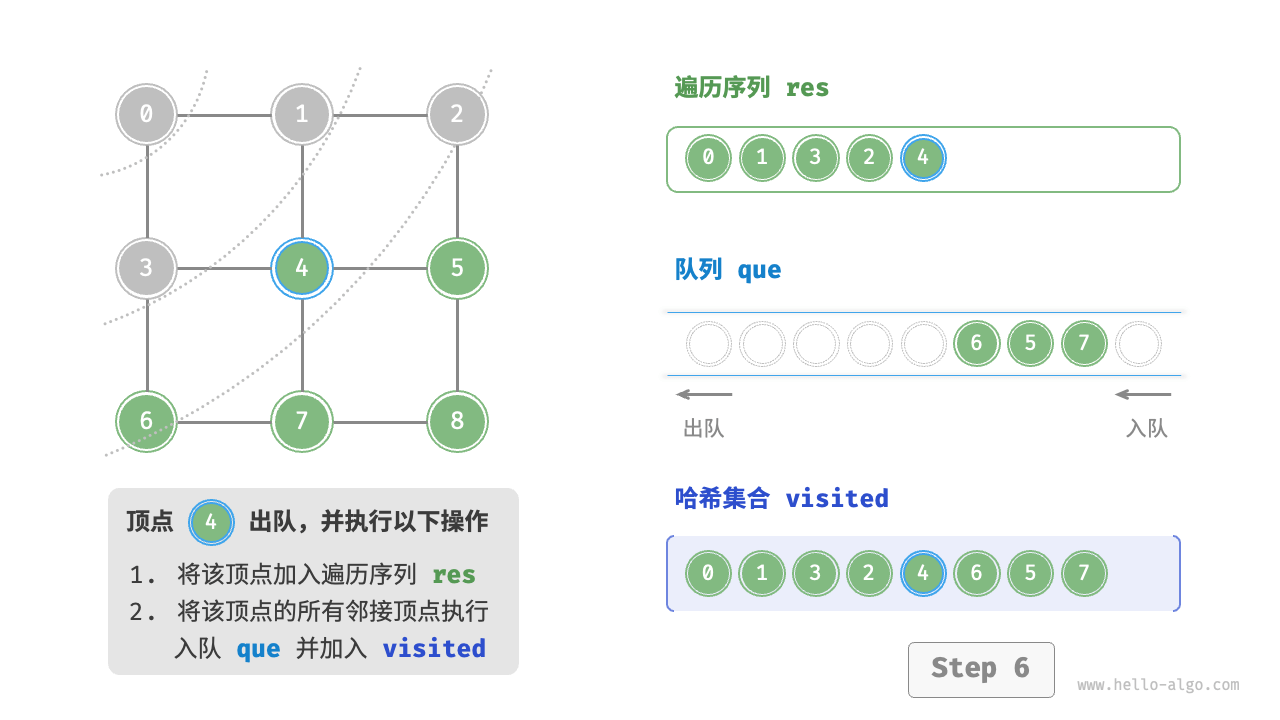
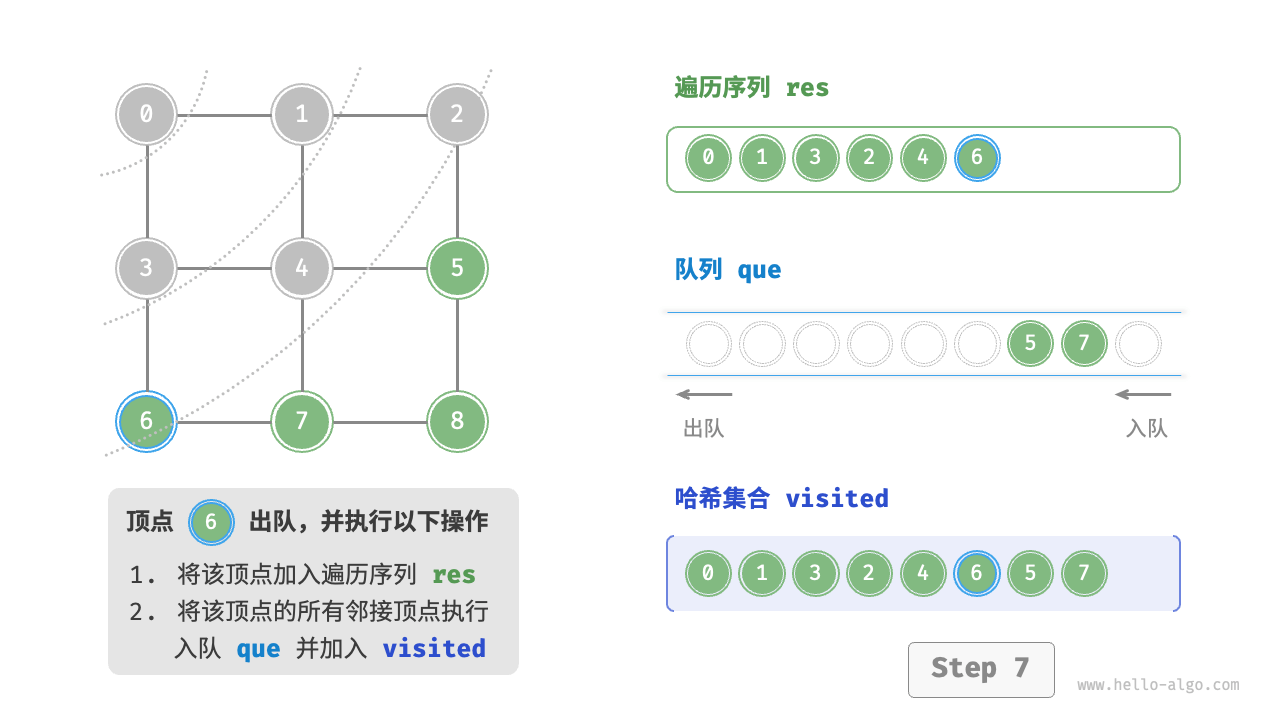
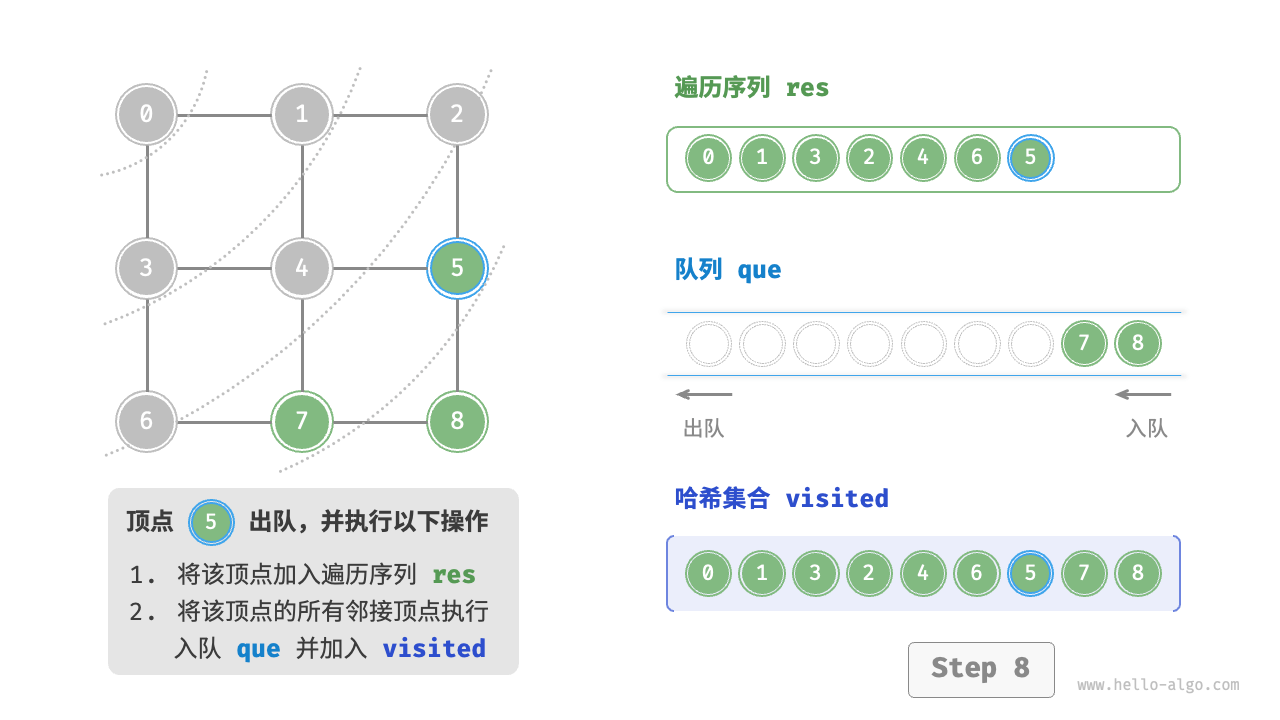
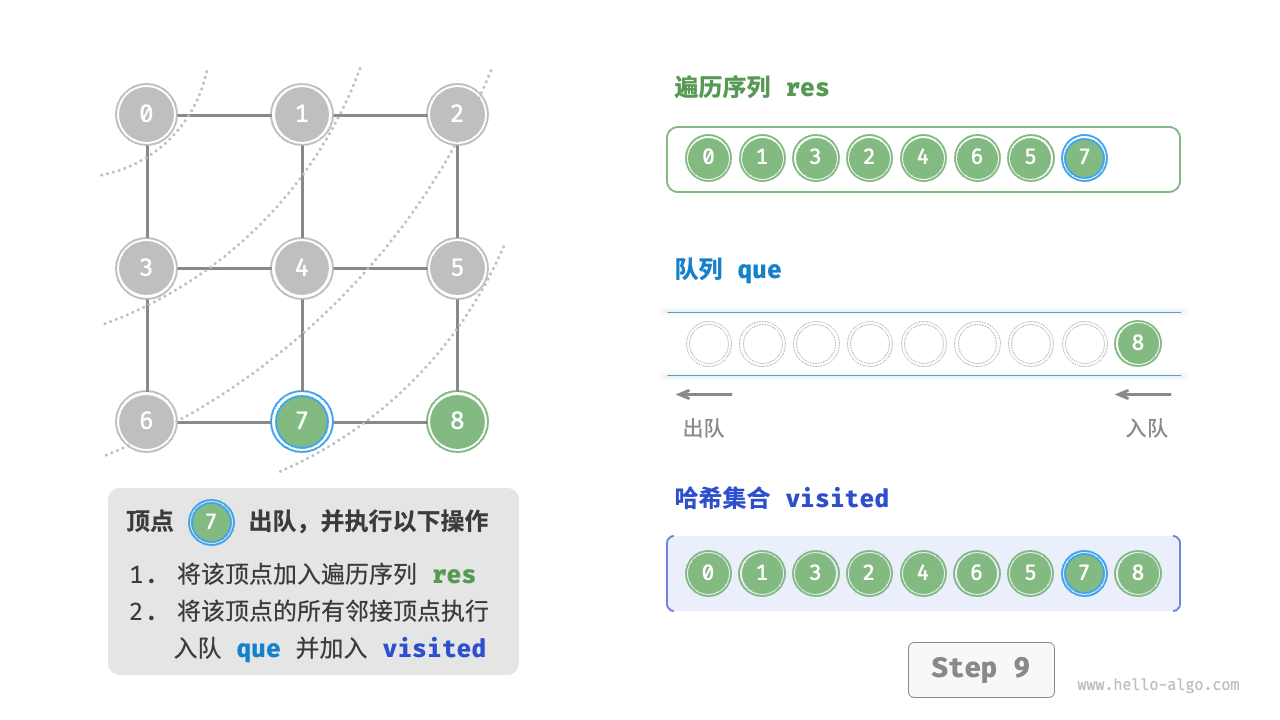
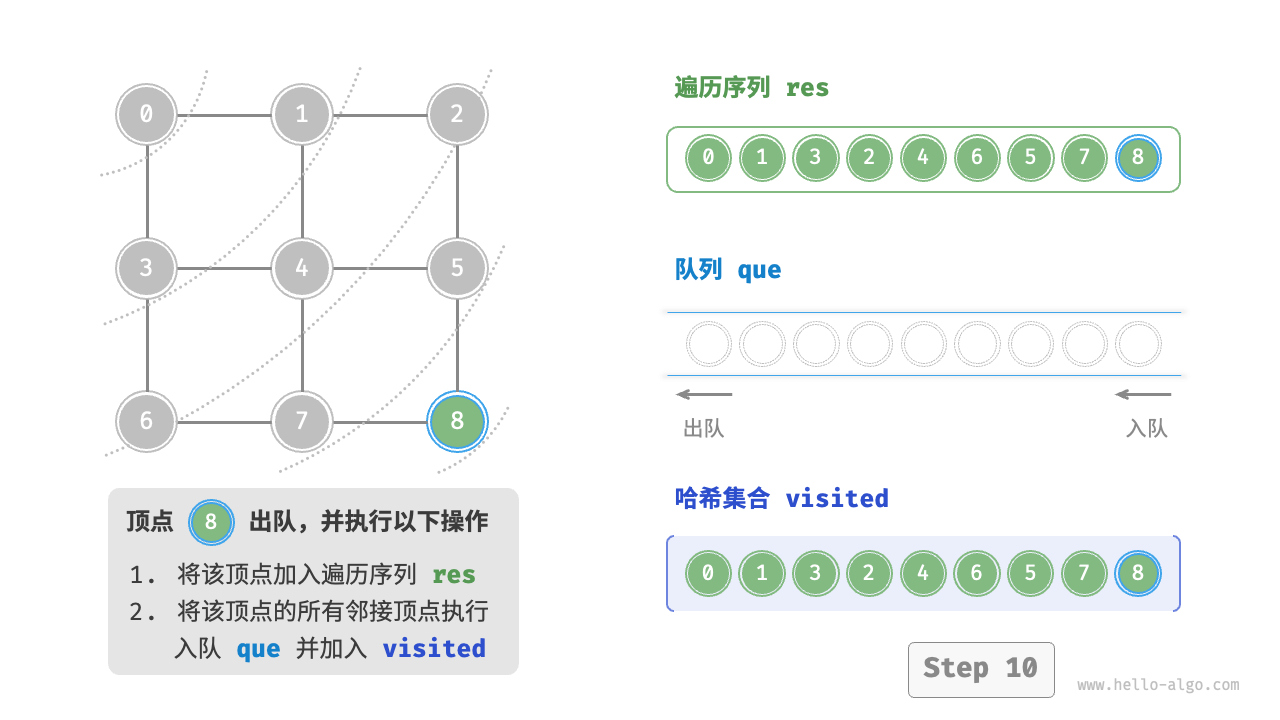
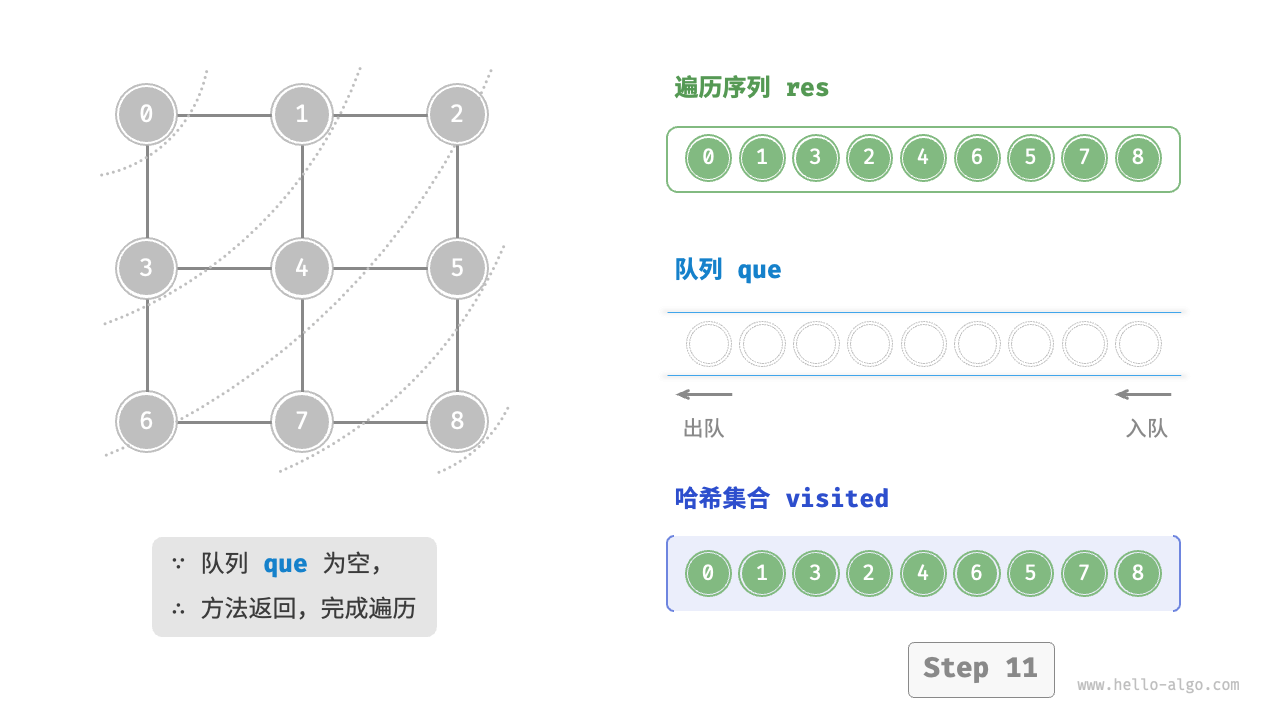
question "广度优先遍历的序列是否唯一?"
不唯一。广度优先遍历只要求按“由近及远”的顺序遍历,而多个相同距离的顶点的遍历顺序允许被任意打乱。以上图为例,顶点 、 的访问顺序可以交换,顶点 、、 的访问顺序也可以任意交换。
# 复杂度分析
时间复杂度:所有顶点都会入队并出队一次,使用 时间;在遍历邻接顶点的过程中,由于是无向图,因此所有边都会被访问 次,使用 时间;总体使用 时间。
空间复杂度:列表 res ,哈希集合 visited ,队列 que 中的顶点数量最多为 ,使用 空间。
# 深度优先遍历
深度优先遍历是一种优先走到底、无路可走再回头的遍历方式。如下图所示,从左上角顶点出发,访问当前顶点的某个邻接顶点,直到走到尽头时返回,再继续走到尽头并返回,以此类推,直至所有顶点遍历完成。
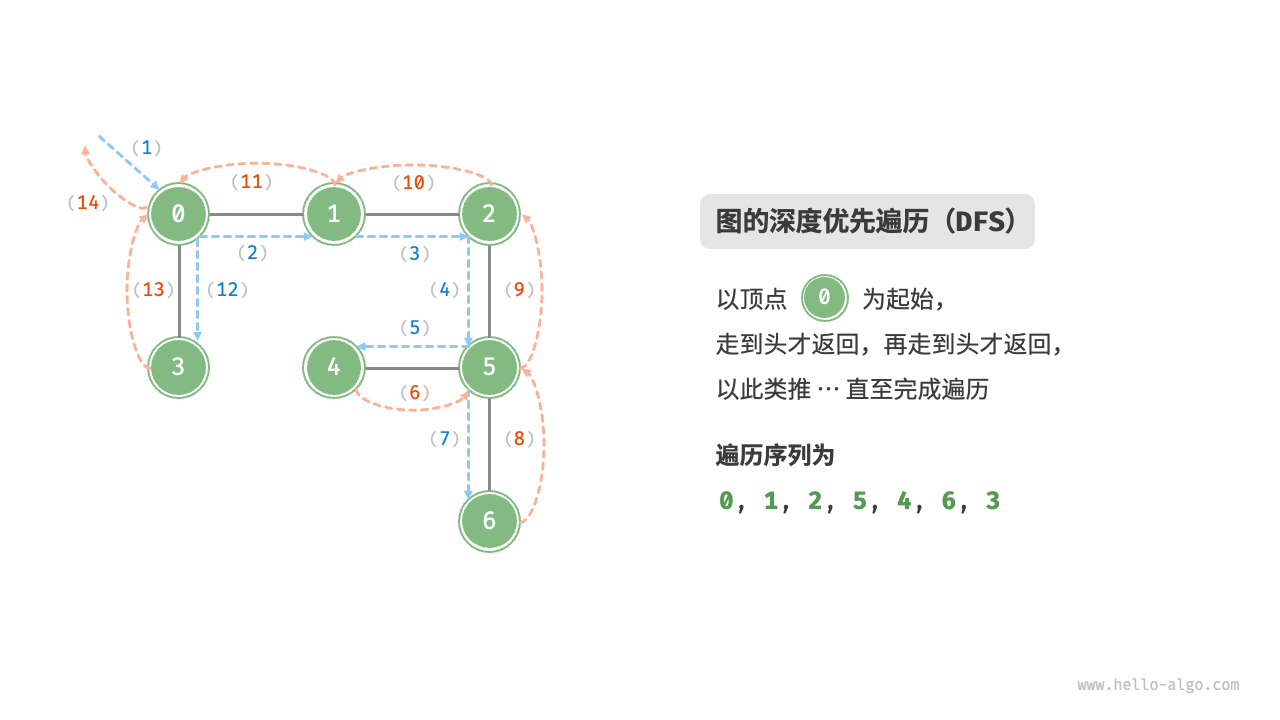
# 算法实现
这种“走到尽头再返回”的算法范式通常基于递归来实现。与广度优先遍历类似,在深度优先遍历中,我们也需要借助一个哈希集合 visited 来记录已被访问的顶点,以避免重复访问顶点。
#include <iostream>
#include <vector>
#include <unordered_set>
using namespace std;
// 结构体表示图的顶点
struct Vertex {
vector<int> neighbors; // 邻接顶点
};
// 深度优先遍历的递归实现
void DFS(int currentVertex, const vector<Vertex>& graph, unordered_set<int>& visited) {
// 标记当前顶点为已访问
visited.insert(currentVertex);
cout << "访问顶点: " << currentVertex << endl;
// 递归访问所有未访问的邻接顶点
for (int neighbor : graph[currentVertex].neighbors) {
if (visited.find(neighbor) == visited.end()) {
DFS(neighbor, graph, visited);
}
}
}
int main() {
// 创建一个包含 6 个顶点的图
int numVertices = 6;
vector<Vertex> graph(numVertices);
// 添加边 (无向图)
graph[0].neighbors.push_back(1);
graph[0].neighbors.push_back(2);
graph[1].neighbors.push_back(0);
graph[1].neighbors.push_back(3);
graph[2].neighbors.push_back(0);
graph[2].neighbors.push_back(3);
graph[3].neighbors.push_back(1);
graph[3].neighbors.push_back(2);
graph[3].neighbors.push_back(4);
graph[4].neighbors.push_back(3);
graph[4].neighbors.push_back(5);
graph[5].neighbors.push_back(4);
// 深度优先遍历 (从顶点 0 开始)
unordered_set<int> visited;
cout << "深度优先遍历的顺序如下:" << endl;
DFS(0, graph, visited);
return 0;
}
# 代码解析:
- DFS 函数:递归地遍历图,从
currentVertex顶点开始,首先标记该顶点为已访问,之后对其所有未访问的邻接顶点递归调用DFS。 - visited 集合:与 BFS 类似,
unordered_set用于记录已经访问的顶点,避免重复访问。 - 邻接表:使用
vector<Vertex>存储图的所有顶点及其邻接顶点列表。 - 主函数
main:构建图并调用DFS函数,从顶点0开始进行深度优先遍历。
# 递归实现:
在这个递归实现中,深度优先遍历会尽可能深入到图的某条路径的尽头,然后回溯到上一个节点,继续尝试其他路径,直到所有顶点都被访问过。这种“先深入,再回溯”的思想是 DFS 的核心。
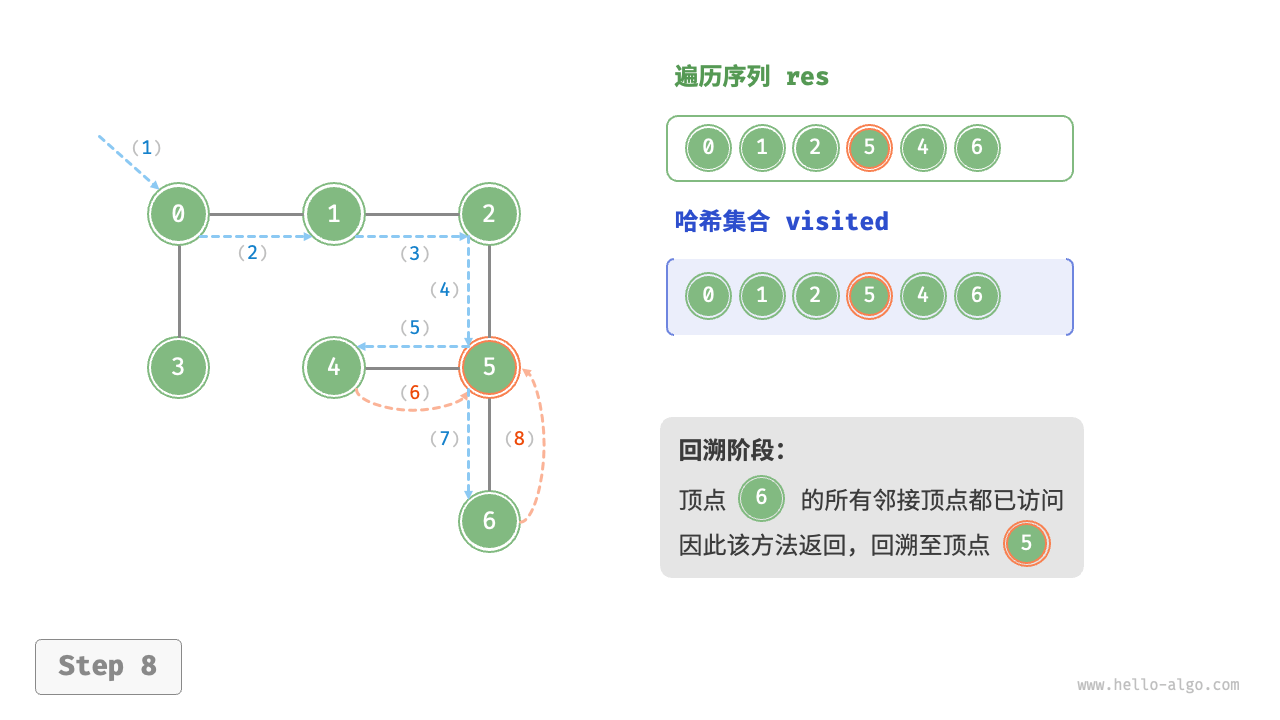
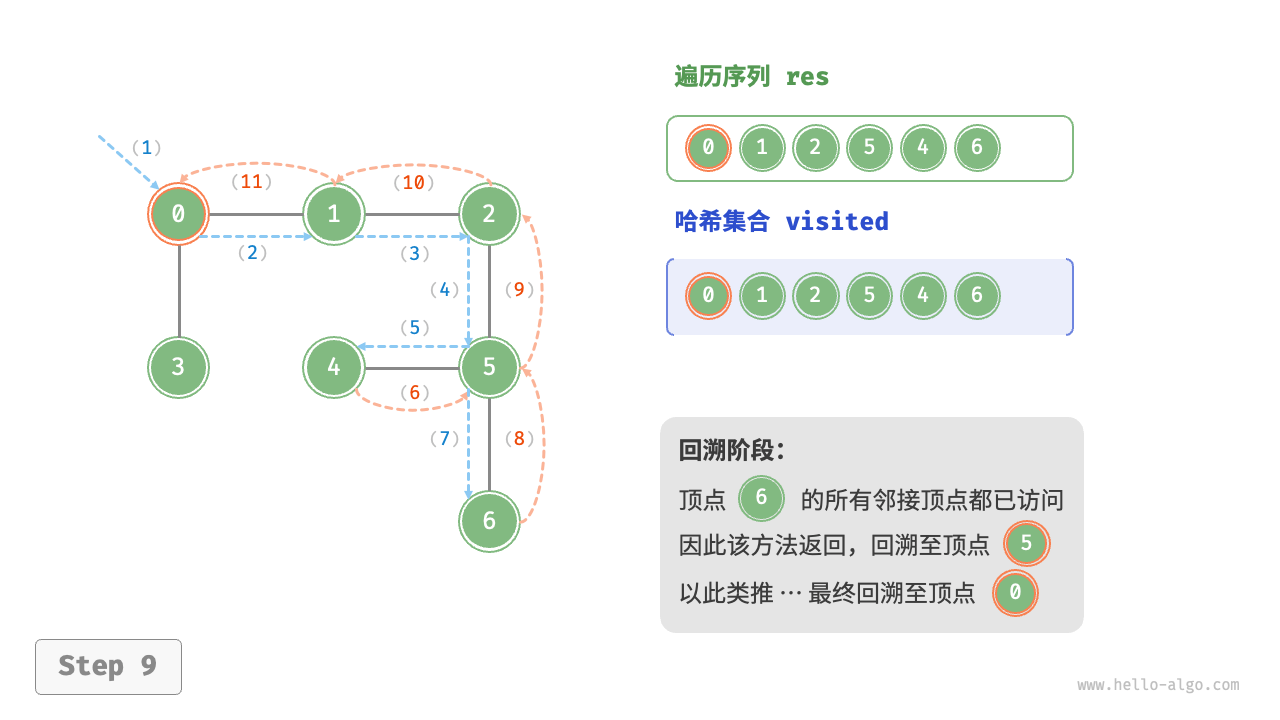
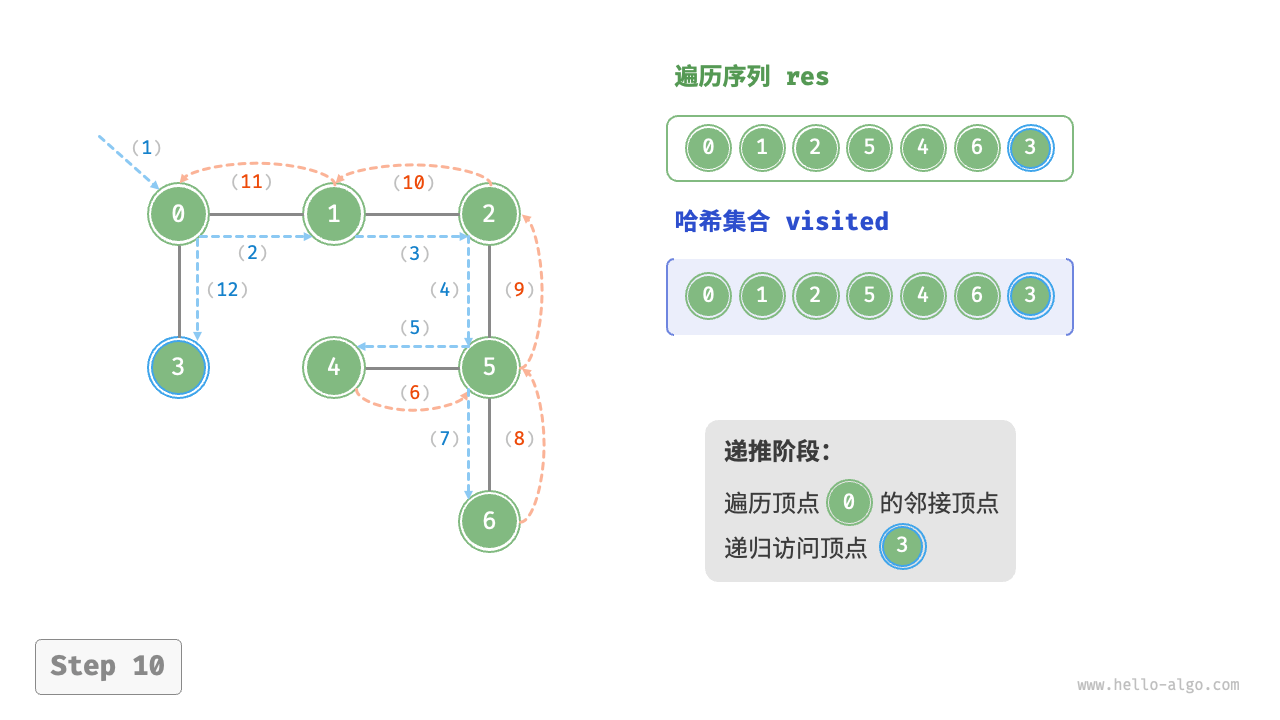
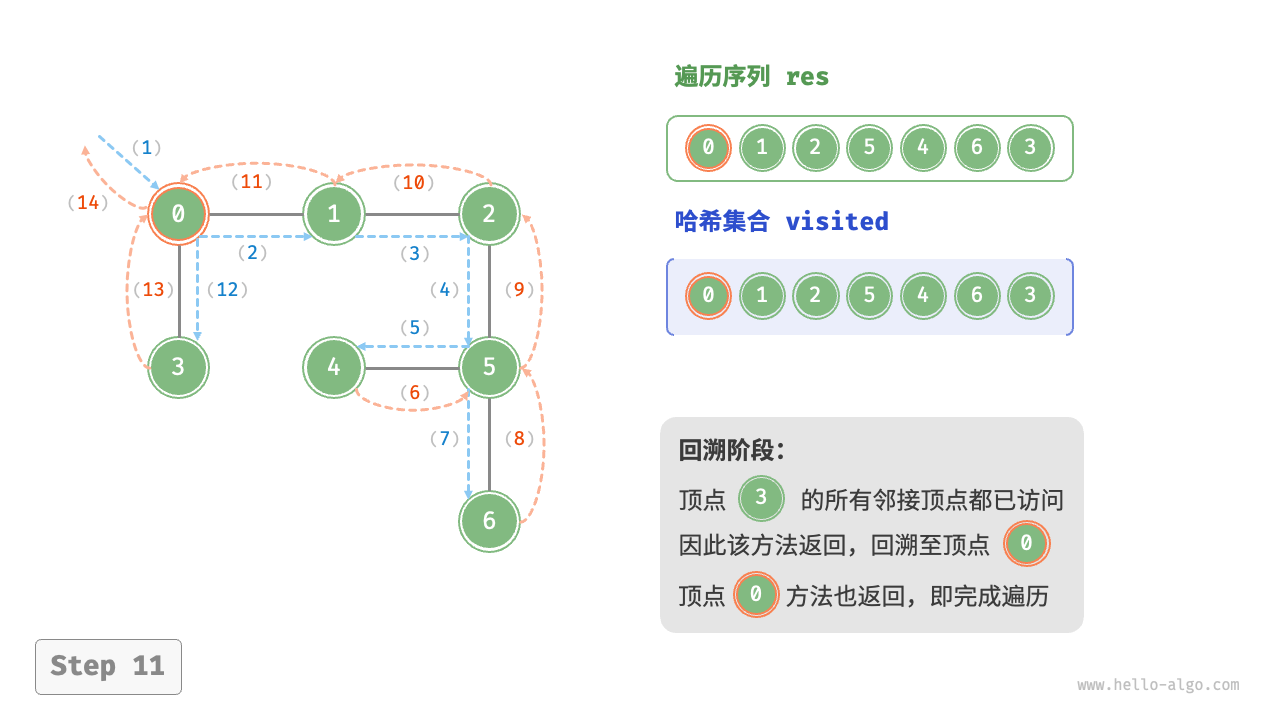
深度优先遍历的算法流程如下图所示。
- 直虚线代表向下递推,表示开启了一个新的递归方法来访问新顶点。
- 曲虚线代表向上回溯,表示此递归方法已经返回,回溯到了开启此方法的位置。
为了加深理解,建议将下图与代码结合起来,在脑中模拟(或者用笔画下来)整个 DFS 过程,包括每个递归方法何时开启、何时返回。
图的深度优先遍历步骤
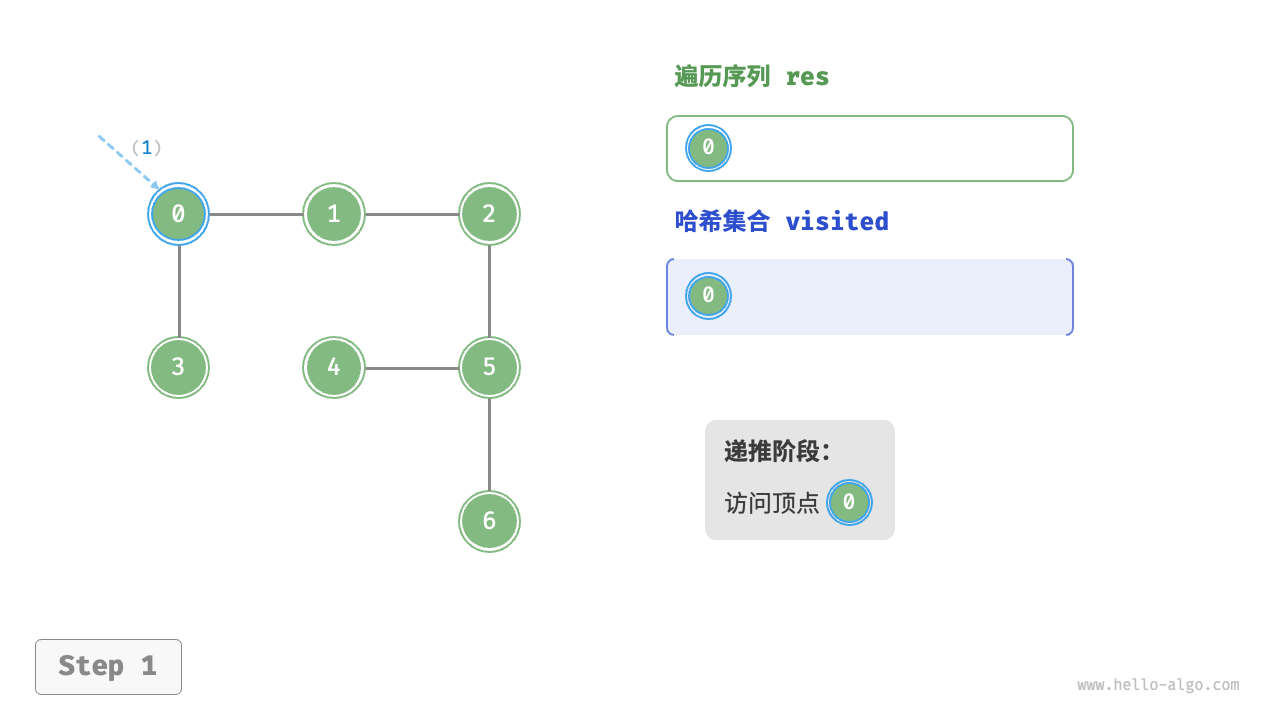
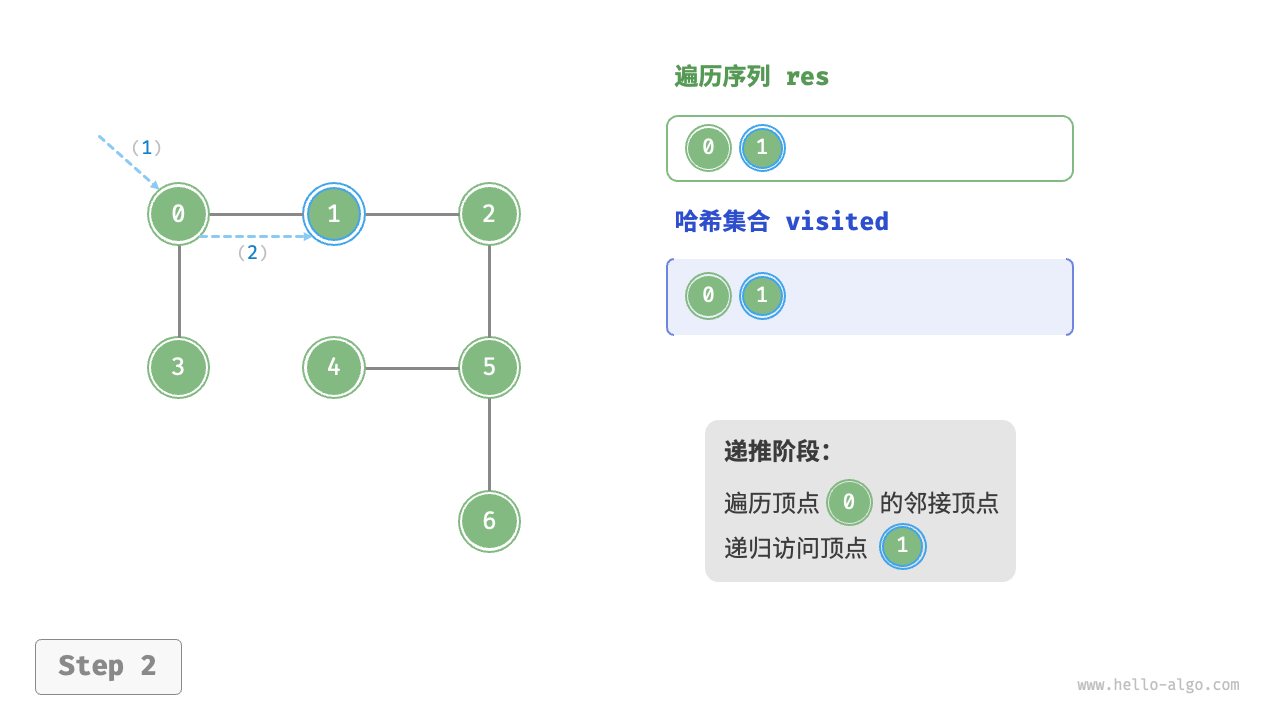
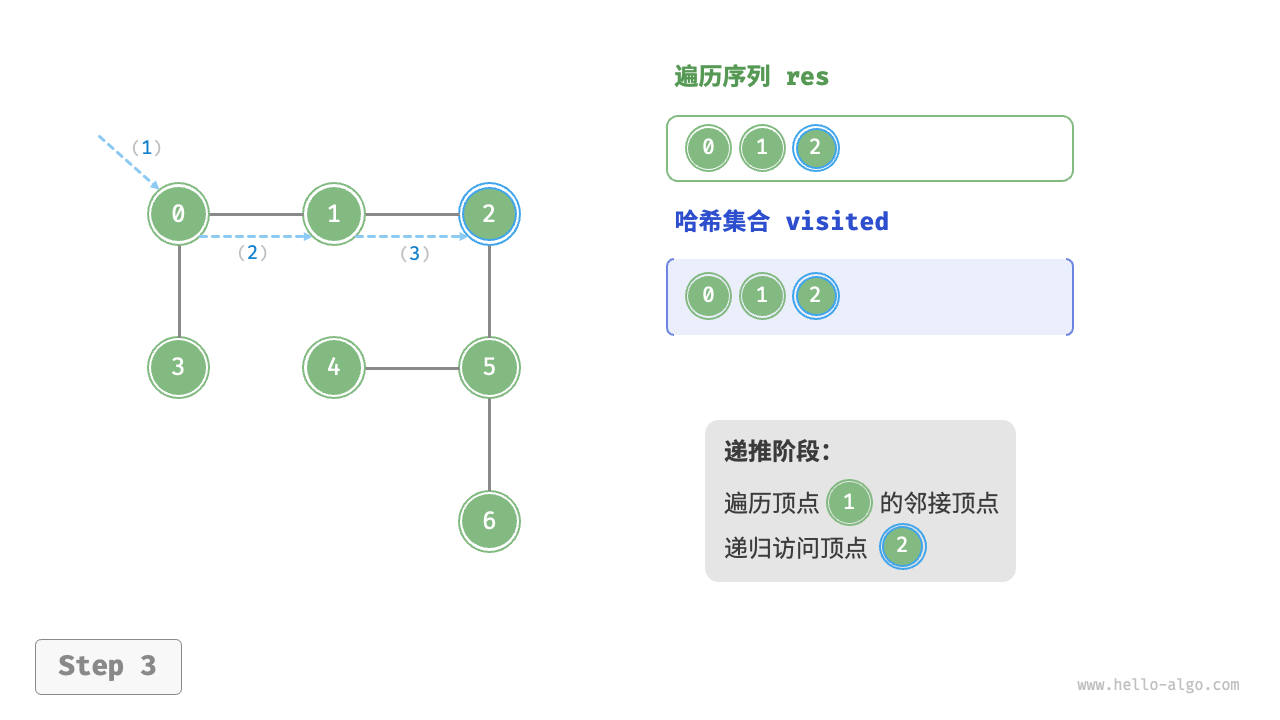
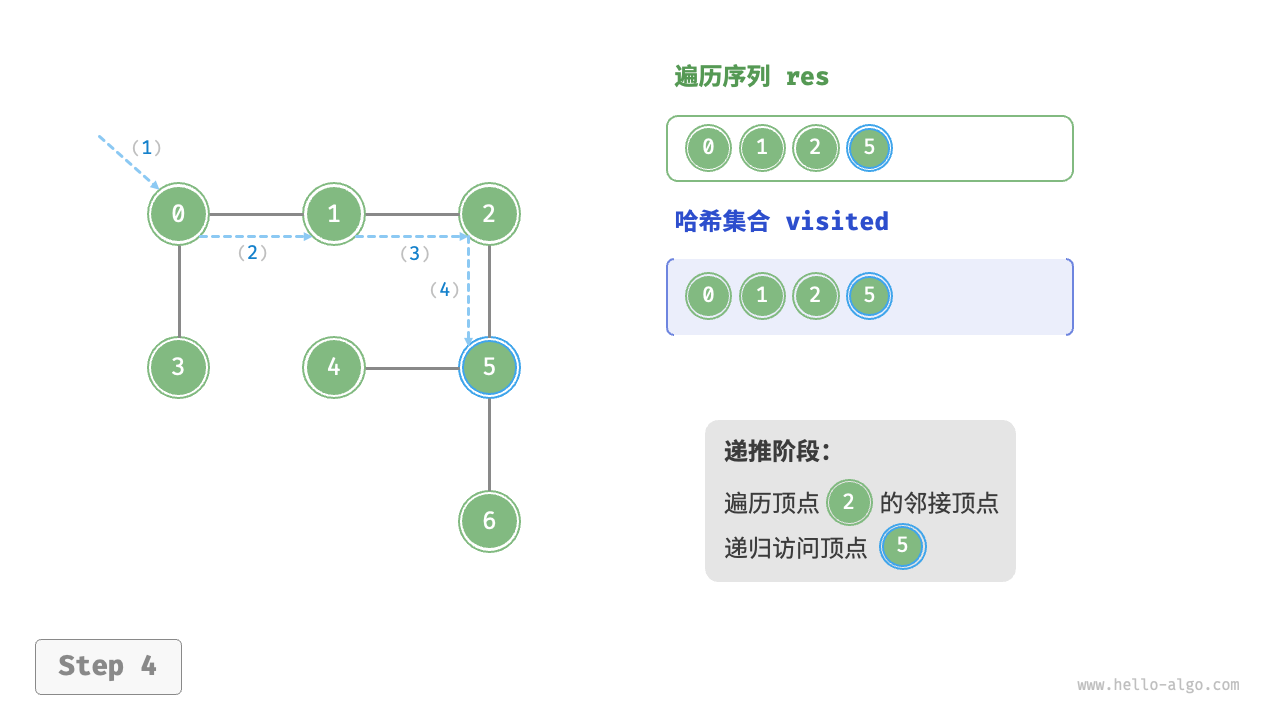
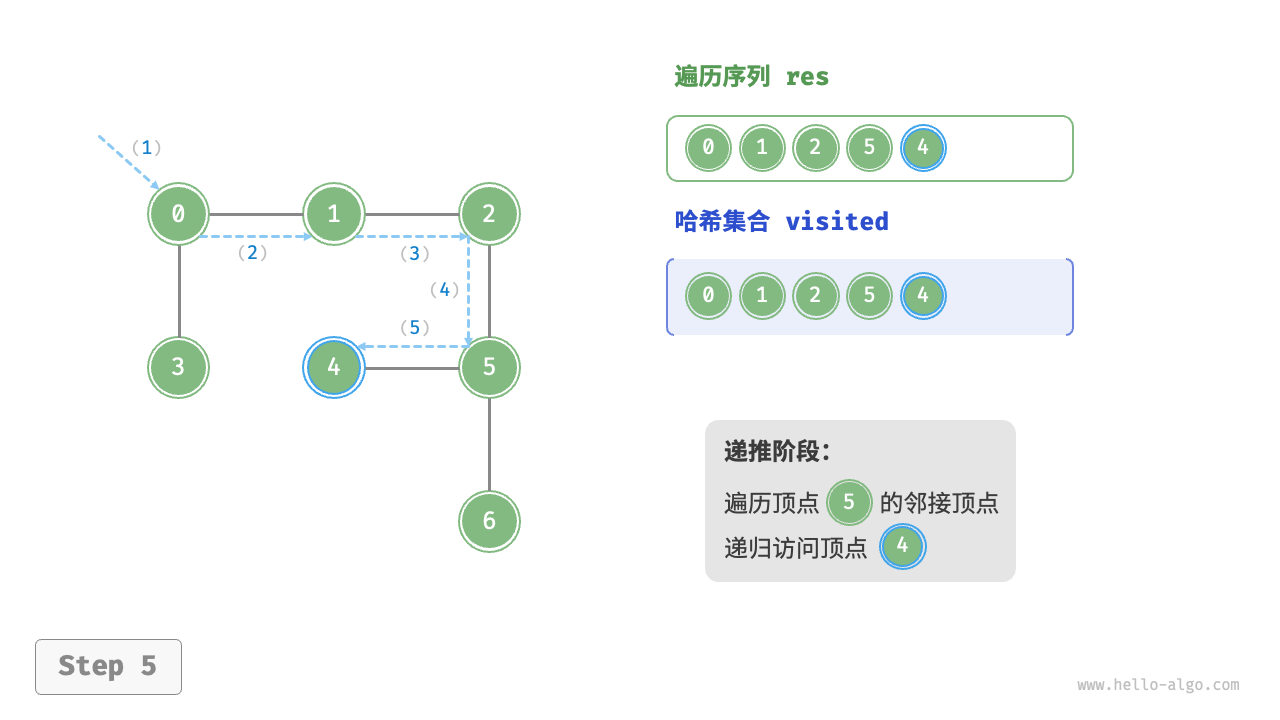
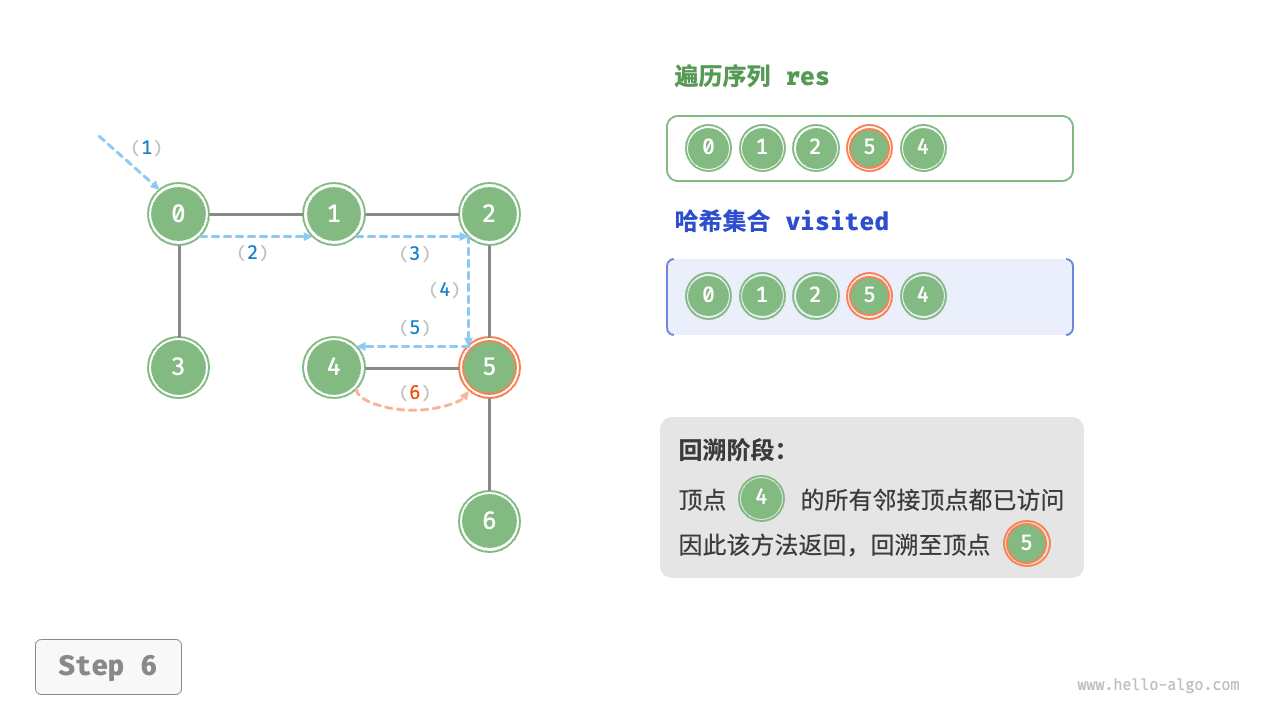
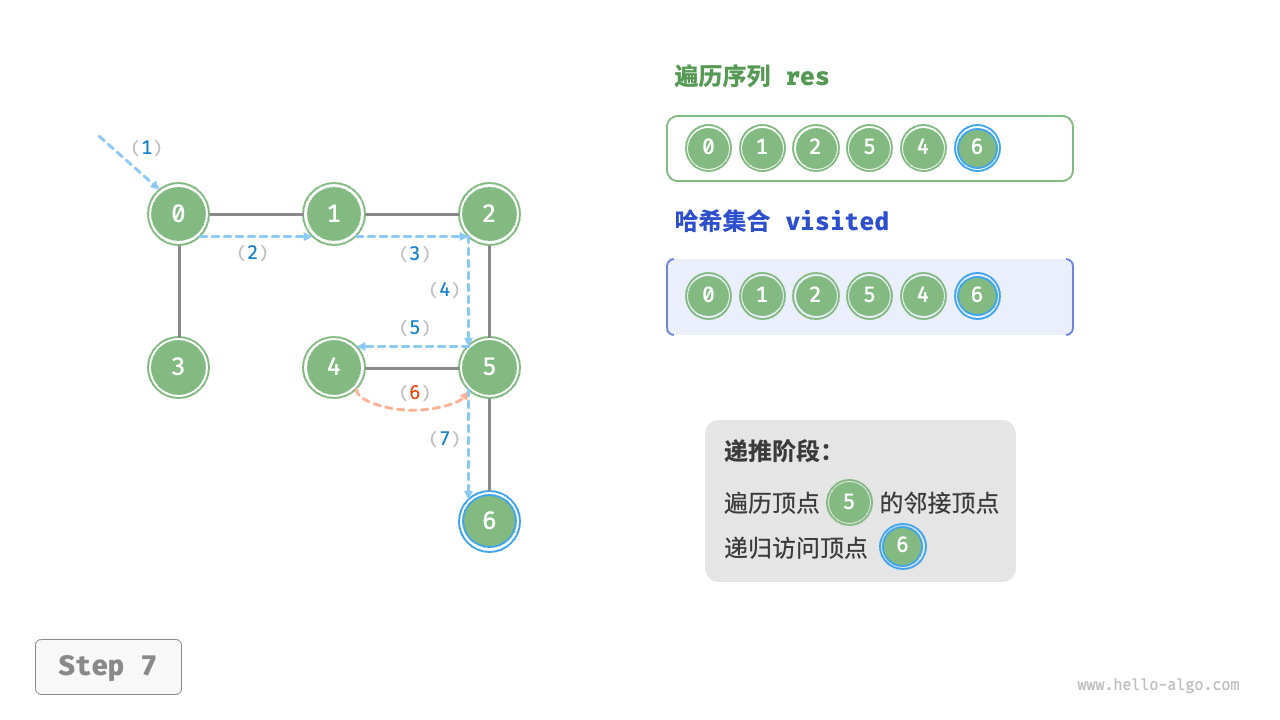
question "深度优先遍历的序列是否唯一?"
与广度优先遍历类似,深度优先遍历序列的顺序也不是唯一的。给定某顶点,先往哪个方向探索都可以,即邻接顶点的顺序可以任意打乱,都是深度优先遍历。
以树的遍历为例,“根 左 右”“左 根 右”“左 右 根”分别对应前序、中序、后序遍历,它们展示了三种遍历优先级,然而这三者都属于深度优先遍历。
# 复杂度分析
时间复杂度:所有顶点都会被访问 次,使用 时间;所有边都会被访问 次,使用 时间;总体使用 时间。
空间复杂度:列表 res ,哈希集合 visited 顶点数量最多为 ,递归深度最大为 ,因此使用 空间。
# 拓扑排序(Topological Sorting)
拓扑排序是一种针对**有向无环图(DAG)**的顶点排序方法。在这种排序中,如果图中存在一条从顶点 到顶点 的路径,那么在排序结果中顶点 一定出现在顶点 的前面。
# 1. 示例
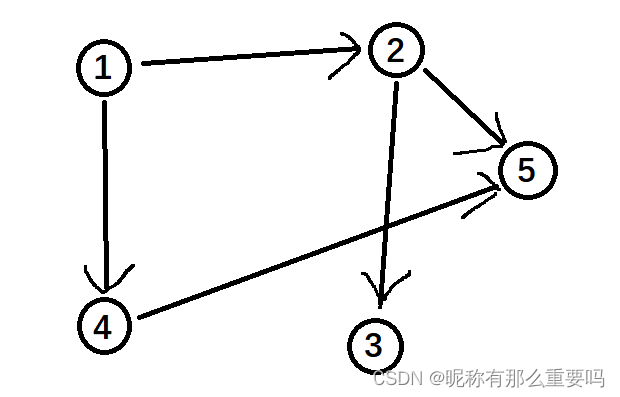
考虑一个简单的有向无环图,其中的边为 , , , 和 。
在所有顶点的排序中,顶点 1 必须在顶点 2 和 4 的前面,顶点 2 必须在顶点 3 和 5 的前面,以此类推。
对于这个图的拓扑排序,可能的序列有:
- 1, 2, 3, 4, 5
- 1, 2, 4, 5, 3
- 1, 4, 2, 3, 5
- 1, 4, 5, 2, 3
只要满足上述条件,序列的具体顺序可以有所不同。在实际应用中,通常会按字典序从小到大输出拓扑排序结果。
# 2. 应用
拓扑排序在实际应用中非常重要,特别是在需要处理具有优先级关系或依赖关系的任务时。例如:
课程安排:如果某门课程需要先修其他课程,那么这些课程和它们之间的先修关系可以用有向无环图表示。拓扑排序可以帮助我们找到一种合理的选课顺序,使得每门课程的先修要求都得到满足。
编译器设计:在编译一个程序时,必须先编译其所依赖的模块。通过拓扑排序,可以确定一个合理的编译顺序,确保所有模块按依赖关系正确编译。
# 3. 实现方法
拓扑排序的实现主要基于图的深度优先搜索(DFS)或广度优先搜索(BFS)。这里介绍基于 BFS 实现的算法,这种方法也称为Kahn 算法。
- Kahn 算法步骤
- 遍历图中的所有顶点,计算每个顶点的入度(即有多少条边指向该顶点)。
- 将所有入度为 0 的顶点加入一个队列,这些顶点没有任何依赖,可以作为拓扑排序的起点。
- 从队列中取出一个顶点,将其加入拓扑排序的结果中,然后遍历其所有邻接顶点,将这些邻接顶点的入度减 1。如果某个邻接顶点的入度变为 0,就将其加入队列。
- 重复步骤 3,直到队列为空。如果图中还有顶点未被访问,说明图中存在环,无法进行拓扑排序。否则,拓扑排序成功。
- 示例步骤
考虑前述图的示例,蓝色数字表示每个顶点的入度。
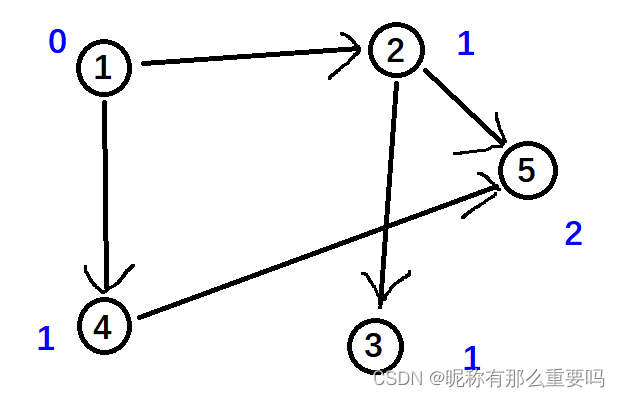
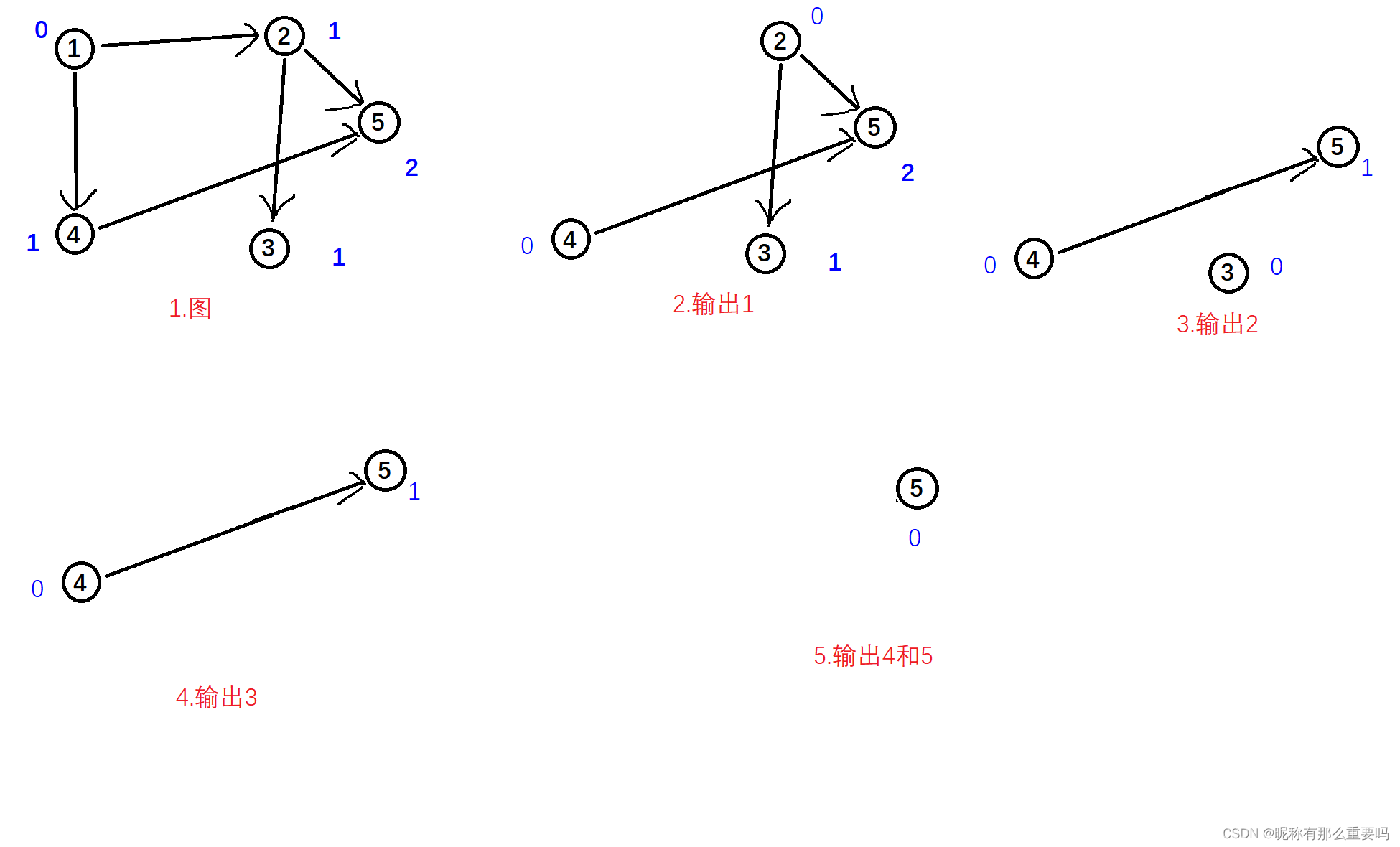
- 将入度为 0 的 1 号顶点加入队列。
- 取出队列中的 1 号顶点,将与其相连的 2、4 号顶点的入度减 1,并输出 1。此时,2、4 号顶点的入度变为 0,因此也加入队列。队列不为空,继续操作。
- 取出队头的 2 号顶点,将与其相连的 3、5 号顶点的入度减 1,并输出 2。3 号顶点的入度变为 0,也加入队列。队列不为空,继续操作。
- 取出队头的 4 号顶点,将与其相连的 5 号顶点的入度减 1,并输出 4。5 号顶点的入度变为 0,也加入队列。队列不为空,继续操作。
- 队列中剩下 3、5 号顶点,依次输出。队列为空,程序结束。
最终输出为“1 2 3 4 5”(字典序最小)。
# 4. C++ 代码实现
以下是使用 BFS 实现的 C++ 代码:
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int n; // 节点个数
int d[10005]; // 入度
vector<int> v[10005]; // vector 存图,方便找到相邻节点
int cur, ans[10005]; // 数组光标和答案数组
void topusort() // 拓扑排序函数
{
queue<int> q; // 入度为 0 的队列
for (int i = 1; i <= n; i++) // 将入度为 0 的节点加入队列
if (d[i] == 0)
q.push(i);
while (!q.empty())
{
int f = q.front(); // 取队头结点
ans[++cur] = f; // 将队头结点加入结果
q.pop(); // 队头出队
for (int i = 0; i < v[f].size(); i++) // 遍历与队头相邻的节点
{
int t = v[f][i]; // 相邻节点编号
d[t]--; // 入度减 1
if (d[t] == 0) // 入度为 0 加入队列
q.push(t);
}
}
}
int main()
{
// 读入图的节点和边
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
int x, y;
cin >> x >> y; // 读入边 x -> y
d[y]++; // 增加 y 的入度
v[x].push_back(y); // 在 x 的邻接表中加入 y
}
topusort(); // 调用拓扑排序
if (cur != n) // 如果结果中节点数不为 n,说明图中有环
printf("图中有环,无法进行拓扑排序!!!\n");
else
{
printf("拓扑排序后的序列:");
for (int i = 1; i <= cur; i++)
printf("%d ", ans[i]); // 输出拓扑排序结果
puts(""); // 换行
}
return 0;
}