讲义

课后作业

2024/1/6

# 第十课

# 1. 编写一个程序，首先输入一个正整数n（不超过 100），然后输入n个整数存入数组。计算这些整数的总和，输出这个总和。

  • 参考答案
#include <iostream>
using namespace std;
int main() {
    int n, sum = 0;
    cin >> n;
    if (n < 1 || n > 100) {
        cout << "输入的数字超出有效范围（1-100）" << endl;
        return 1;
    }
    int numbers[100];
    for (int i = 0; i < n; i++) {
        cin >> numbers[i];
    }
    for (int i = 0; i < n; i++) {
        sum += numbers[i];
    }
    cout << "总和: " << sum << endl;
    return 0;
}
// 使用 vector 的版本
#include <iostream>
#include <vector>
using namespace std;
int main() {
    int n, sum = 0;
    cin >> n;
    if (n < 1 || n > 100) {
        cout << "输入的数字超出有效范围（1-100）" << endl;
        return 1;
    }
    // vector 的大小是动态指定的
    vector<int> numbers(n);
    for (int i = 0; i < n; i++) {
        cin >> numbers[i];
    }
    for (int i = 0; i < n; i++) {
        sum += numbers[i];
    }
    cout << "总和: " << sum << endl;
    return 0;
}
  • 历史解析
    • 在不使用vector的情况下，int arrow[n] 其中 n 是在运行时确定的,在标准环境下运行会引发错误，在 C++中，使用标准数组时其大小必须是常量表达式。这意味着数组的大小需要在编译时就确定，而不是在运行时。
    • 使用var作为变量名在 C++中不算错误，但是应尽量避免命名时涉及关键字相关
    • 最后的循环在已知输入数量下可以改进循环

# 2. 编写一个程序，首先输入一个正整数n（不超过 100），然后输入n个整数存入数组。找出这些整数中的最大值，输出这个最大值。

  • 参考答案
#include <iostream>
using namespace std;
int main() {
    int n;
    cout << "请输入整数的数量（不超过100）: ";
    cin >> n;
    if (n <= 0 || n > 100) {
        cout << "输入的整数数量不合法。" << endl;
        return 1;
    }
    int numbers[100];
    cout << "请输入" << n << "个整数：" << endl;
    for (int i = 0; i < n; i++) {
        cin >> numbers[i];
    }
    int max_value = numbers[0];
    for (int i = 1; i < n; i++) {
        if (numbers[i] > max_value) {
            max_value = numbers[i];
        }
    }
    cout << "最大值为：" << max_value << endl;
    return 0;
}
  • 历史解析
    • 注意题目要求存入数组

# 3. 编写一个程序，首先输入一个正整数n（不超过 100），然后输入n个整数存入数组。检查数组中的每一个数字是否是素数。输出每个数字及其是否为素数的信息(逐个打印)。

利用讲义的搜索功能查找之前习题中提及的素数概念

  • 参考答案
#include <iostream>
using namespace std;
int main() {
    int n;
    cout << "请输入一个正整数n（不超过100）：";
    cin >> n;
    int arr[100];
    cout << "请输入" << n << "个整数：" << endl;
    for (int i = 0; i < n; ++i) {
        cin >> arr[i];
    }
    for (int i = 0; i < n; ++i) {
        bool isPrime = true;
        if (arr[i] <= 1) {
            isPrime = false;
        } else {
            // 从 2 开始，一直检查到 j 的平方不超过 arr[i]
            for (int j = 2; j * j <= arr[i]; ++j) {
                if (arr[i] % j == 0) {
                    isPrime = false;
                    break;
                }
            }
        }
        cout << arr[i] << (isPrime ? "是素数" : "不是素数") << endl;
    }
    return 0;
}

  1. 素数的定义：素数是只有 1 和它本身两个正因子的大于 1 的自然数。

  2. 非素数（合数）的因子：如果一个数 N 是合数（非素数），那么它可以被分解为两个因子的乘积，即 N = a * b。如果这两个因子 a 和 b 都大于 N 的平方根，那么他们的乘积 a * b 将会大于 N，这与假设 N = a * b 矛盾。因此，如果 N 是合数，它必然有一个因子不大于其平方根。

  3. 检查范围的优化：基于以上性质，当检查一个数是否为素数时，我们只需要检查到其平方根即可。如果在这个范围内没有找到除 1 和它本身之外的因子，我们可以断定该数是素数。

# 4. 编写一个程序，首先输入两个正整数n（不超过 100）和k，然后输入n个整数存入数组。将数组中的元素循环右移k个位置（例如，数组[1,2,3,4,5]右移 2 位后变为[4,5,1,2,3]），然后输出右移后的数组元素(逐个打印)。

  • 参考答案
#include <iostream>
using namespace std;
int main() {
    int n, k;
    cout << "请输入n和k的值：";
    cin >> n >> k;
    int arr[100], newArr[100];
    cout << "请输入" << n << "个整数：";
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }
    // 处理k大于n的情况
    // k %= n;
    for (int i = 0; i < n; i++) {
        newArr[(i + k) % n] = arr[i];
    }
    cout << "右移后的数组元素为：";
    for (int i = 0; i < n; i++) {
        cout << newArr[i] << " ";
    }
    return 0;
}

  1. k %= n;：

    这行代码是为了处理当k（右移的位数）大于或等于n（数组的长度）的情况。由于右移n个位置的数组会回到原始状态，右移n + 1个位置的效果与右移1个位置相同，因此可以通过取模运算k %= n来得到与原始右移相同效果的最小非负右移位数。例如，如果数组长度为5，右移7位与右移2位的效果相同，因为7 % 5 = 2。

  2. for (int i = 0; i < n; i++) { newArr[(i + k) % n] = arr[i]; }：

    这个循环是用来将原始数组arr中的每个元素移动到新数组newArr中正确的位置。循环变量i遍历了原数组的每一个索引。

    • newArr[(i + k) % n] = arr[i];：这行代码实现了元素的右移。对于原数组arr中索引为i的元素，其在新数组newArr中的位置是(i + k) % n。

      这里，(i + k) % n计算出右移k位后元素的新位置。由于使用了模运算% n，当(i + k)大于或等于n时，它会正确地回绕到数组的开始，从而实现循环右移的效果。

举个例子，假设数组为[1, 2, 3, 4, 5]，n = 5，k = 2。循环中的操作将会是：

  • 当i = 0（即元素1）时，newArr[(0 + 2) % 5] = arr[0]，即newArr[2] = 1。
  • 当i = 1（即元素2）时，newArr[(1 + 2) % 5] = arr[1]，即newArr[3] = 2。
  • 以此类推，直到循环结束。

# 5. 编写一个程序，首先输入两个正整数 n 和 m（均不超过 100），分别表示两个数组的长度。然后分别输入这两个数组的元素。合并这两个数组为一个新的正序排列数组，并输出合并后的数组(逐个打印)。

  • 参考答案
#include <iostream>
using namespace std;
int main() {
    int n, m;
    cout << "请输入第一个数组长度：";
    cin >> n;
    int arr1[100];
    cout << "请输入第一个数组内容：";
    for (int i = 0; i < n; i++) {
        cin >> arr1[i];
    }
    cout << "请输入第二个数组长度：";
    cin >> m;
    int arr2[100];
    cout << "请输入第二个数组内容：";
    for (int i = 0; i < m; i++) {
        cin >> arr2[i];
    }
    int combined[200];
    for (int i = 0; i < n; i++) {
        combined[i] = arr1[i];
    }
    for (int i = 0; i < m; i++) {
        combined[n + i] = arr2[i];
    }
    int size = n + m;
    // 简单的冒泡排序
    for (int i = 0; i < size - 1; i++) {
        for (int j = 0; j < size - i - 1; j++) {
            if (combined[j] > combined[j + 1]) { // 相邻元素两两对比
                // 交换元素
                int temp = combined[j];
                combined[j] = combined[j + 1];
                combined[j + 1] = temp;
            }
        }
    }
    cout << "正序排列数组: ";
    for (int i = 0; i < n + m; i++) {
        cout << combined[i] << " ";
    }
    cout << endl;
    return 0;
}
10-1

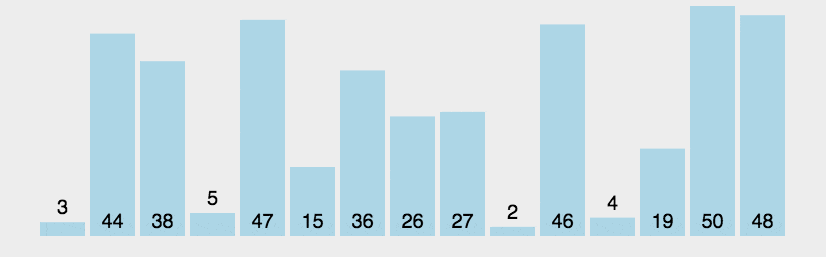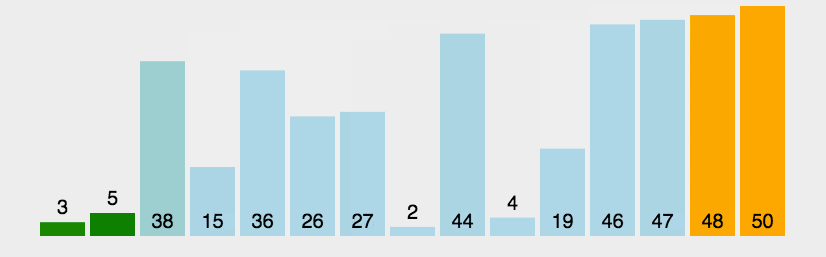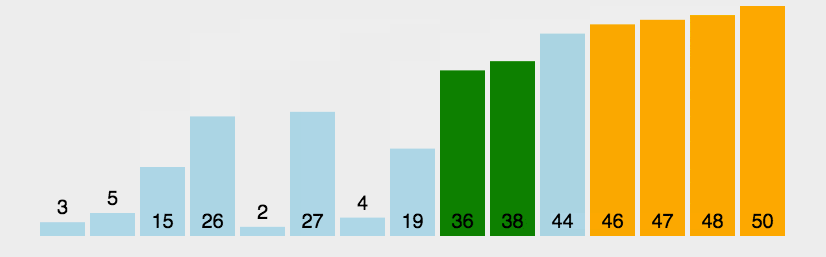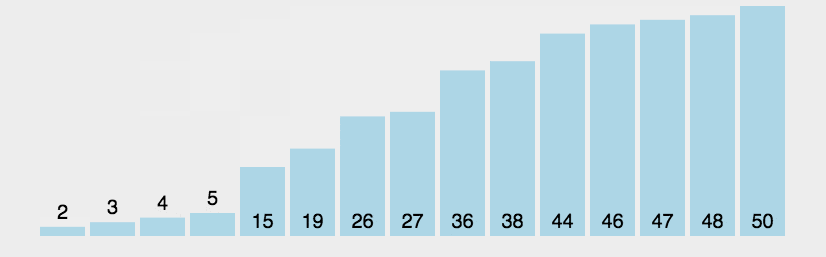
冒泡排序是一种简单的排序算法，它重复地遍历要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复进行的，直到没有再需要交换的元素为止，这时数列就排序完成了。

  1. 外层循环 (for (int i = 0; i < size - 1; i++)):

    • 这个循环控制整个排序过程中需要进行多少轮比较。因为每一轮至少可以确保将一个最大的元素移动到正确的位置，所以需要进行 size - 1 轮比较（其中 size 是数组 combined 的长度）。

  2. 内层循环 (for (int j = 0; j < size - i - 1; j++)):

    • 内层循环负责在每一轮中，通过比较和交换相邻的元素，将较大的元素“冒泡”到数列的末尾。
    • 随着每一轮的进行，最后的元素将被正确排序，因此每一轮比较的次数会减少。这就是为什么循环条件是 j < size - i - 1，因为最后 i 个元素已经排序好了，无需再次比较。

  3. 比较和交换 (if (combined[j] > combined[j + 1])):

    • 在内层循环中，代码会比较相邻的两个元素 (combined[j] 和 combined[j + 1])。
    • 如果它们的顺序是错误的（即 combined[j] 大于 combined[j + 1]），那么就将它们交换位置。这个过程就像较大的元素在水中冒泡一样，逐渐移动到数列的末端。
上次更新: 2024-10-19 10:01:51

第十一课