课后作业

第三十三课

如无过程，上传图片中阐明思路也可以，或者涉及哪些知识点，也可以写出来

1. 假设字母表{a，b，c，d，e}在字符串出现的频率分别为10%，15%，30%，16%，29%若使用哈夫曼编码方式对字母进行不定长的二进制编码，字母d的编码长度为( )位

• A. 1
• B. 2
• C. 2 或 3
• D. 3

• ✅
• 历史解析:
  • 正确答案：B 、2
  • 哈夫曼编码是一种变长编码，出现频率高的字符编码短，出现频率低的字符编码长, 通过构造哈夫曼树，得到每个字符的编码,之后数出d的编码长度即可

2. 一棵有n个结点的完全二叉树用数组进行存储与表示，已知根结点存储在数组的第1个位置。若存储在数组第9个位置的结点存在兄弟结点和两个子结点，则它的兄弟结点和右子结点的位置分别是( )

• A. 8、18
• B. 18、18
• C. 8、19
• D. 10、19

• ✅
• 历史解析:
  • 正确答案：C 、8、19
  • 完全二叉树的性质：若某结点的位置为i，则其左子结点的位置为2i，右子结点的位置为2i+1，父结点的位置为i/2，因此第9位置结点一定是第4结点的右孩子（左孩子下标都是偶数，右孩子下标都是奇数）。该结点的兄弟结点是4的左孩子，在数组中的下标应该比9少1，为8。9的右孩子的下标为9*2+1=19。
  • 所以结点9的兄弟结点的位置为8，右子结点的位置为19

3. 考虑由N个顶点构成的有向连通图，采用邻接矩阵的数据结构表示时，该矩阵中至少存在( )个非零元素

• A. N-1
• B. N
• C. N+1
• D. $N^2$

• ❌
• 历史解析:
  • 正确答案：A 、N-1
  • 有向连通图，分为强连通图、单向连通图、弱连通图。若把有向边都当做无向边，如果这个无向图是连通图，那么这个图是弱连通图
  • n个顶点的无向图，最少有n-1条边。那么这个有向图中最少有n-1条边，就可以构成弱连通图。有向图中每条边在邻接矩阵中就是一个元素，占一个位置，因此至少存在n-1个非零元素

4. 对于有n个顶点、m 条边的无向连通图(m>n)，需要删掉( )条边才能使其成为一棵树

• A. m-1
• B. m-n
• C. m-n-1
• D. m-n+1

• ✅
• 历史解析:
  • 正确答案：D 、m-n+1
  • 一棵树是一个无环连通图，即一个无向图是一棵树，当且仅当它是连通的且边数等于顶点数减一。所以对于有n个顶点、m 条边的无向连通图(m>n)，需要删掉m-n+1条边才能使其成为一棵树
  • 也可以这样理解，n个节点的树有 n-1 条边，则需要留下 n-1 条边，即需要删除m-(n-1)条边

5. 以a为起点，对以下的无向图进行深度优先遍历，则b、c、d、e四个点中有可能作为最后一个遍历到的点的个数为( )

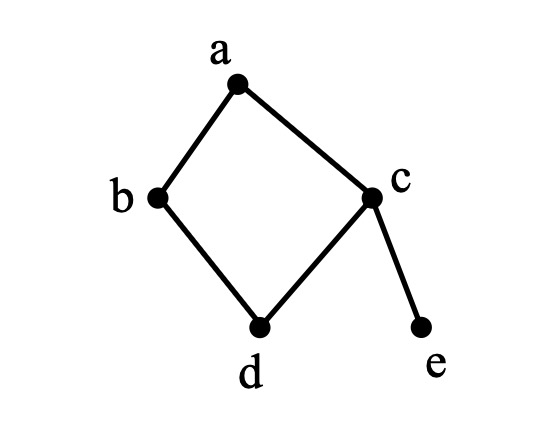
• A. 1
• B. 2
• C. 3
• D. 4

• ❌
• 历史解析:
  • 正确答案：B 、2
  • 从 a 出发，可以选择访问 b 或 c
  • 假设选择访问 b，然后访问 b 的邻接顶点 d，之后再回到 a
  • 接下来访问 c，再依次访问 e 或 d，直到完成遍历
  • 可能的情况：
  1. 路径 1：a -> b -> d -> c -> e
     • 最后一个遍历到的点是 e
  2. 路径 2：a -> c -> e -> d -> b
     • 最后一个遍历到的点是 b
  3. 路径 3：a -> c -> d -> b -> e
     • 最后一个遍历到的点是 e
  • 从这两个可能的路径可以看出，只有 b 和 e 有可能作为最后一个遍历到的点
  • 在深度优先遍历中，b 和 e 是两个可能作为最后一个遍历到的点。因此，正确答案是2 个