真题考试

2024/6/15

考试时间：2 小时

满分100分。请在作答。不得使用任何电子设备（如计算器、手机、电子词典等）或查阅任何书籍资料。

# 一、单项选择题（共15题，每题2分，共计30分）

在C++中，下面哪个关键字用于声明一个变量，其值不能被修改？（）
- A. unsigned
- B. const
- C. static
- D. mutable

答案：B 、const
解析：

A. unsigned：unsigned 是一种数据类型修饰符，用于声明无符号整数类型变量，即只能表示非负整数，不能表示负数。例如，unsigned int 表示无符号整型变量。
B. const：const 在C++中，使用关键字const声明的变量是常量，其数值不能被修改。
C. static：static 是一个关键字，具有多种用途。在变量声明中，static 可以用于声明静态变量，静态变量在程序运行期间只会被初始化一次，其值在函数调用之间保持不变。在函数内部使用 static 修饰的变量，其生命周期会延长到整个程序运行结束。
D. mutable：mutable 是一个关键字，用于声明类的成员变量，在 const 成员函数中，mutable 修饰的变量可以被修改。通常用于需要在 const 成员函数中修改的变量。

八进制数12345670(8进制) 和07654321(8进制)的和为（）
- A. 22222221(8进制)
- B. 21111111(8进制)
- C. 22111111(8进制)
- D. 22222211(8进制)

答案：D 、 22222211(8进制)
解析：要计算八进制数的和，首先将两个八进制数转换为十进制数，然后将其相加，最后将结果转换回八进制数。
八进制数12345670转换为十进制数为：1 * 8^7 + 2 * 8^6 + 3 * 8^5 + 4 * 8^4 + 5 * 8^3 + 6 * 8^2 + 7 * 8^1 + 0 * 8^0 = 3423912
八进制数07654321转换为十进制数为：0 * 8^7 + 7 * 8^6 + 6 * 8^5 + 5 * 8^4 + 4 * 8^3 + 3 * 8^2 + 2 * 8^1 + 1 * 8^0 = 2054353
将两个十进制数相加：3423912 + 2054353 = 5478265
最后将结果5478265转换为八进制数为：2 * 8^7 + 2 * 8^6 + 2 * 8^5 + 2 * 8^4 + 2 * 8^3 + 2 * 8^2 + 1 * 8^1 + 1 * 8^0 = 22222211(8进制)
因此，答案为 D. 22222211(8进制)。

阅读下述代码，请问修改data的value成员以存储3.14，正确的方式是（）
```
union Data{
    int num;
    float value;
    char symbol;
};
union Data data;
```
- A. data.value = 3.14;
- B. value.data = 3.14;
- C. data->value = 3.14;
- D. value->data = 3.14;

答案：A 、 data.value = 3.14;
解析：联合体（union）是一种特殊的数据结构，它允许在相同的内存位置存储不同的数据类型。联合体中的所有成员共享同一块内存空间，因此只能同时存储一个成员的值。在这个例子中，联合体 Data 包含三个成员：int 类型的 num、float 类型的 value 和 char 类型的 symbol。要修改 value 成员的值为 3.14，应该使用 data.value = 3.14; 这种方式。

假设有一个链表的节点定义如下：
```
struct Node {
    int data;
    Node* next;
};
```
现在有一个指向链表头部的指针：Node* head。如果想要在链表中插入一个新节点，其成员data的值为42，并使新节点成为链表的第一个节点，下面哪个操作是正确的？（）
- A. Node* newNode = new Node; newNode->data = 42; newNode->next = head; head = newNode;
- B. Node* newNode = new Node; head->data = 42; newNode->next = head; head = newNode;
- C. Node* newNode = new Node; newNode->data = 42; head->next = newNode;
- D. Node* newNode = new Node; newNode->data = 42; newNode->next = head;

答案：A 、 Node* newNode = new Node; newNode->data = 42; newNode->next = head; head = newNode;
解析：要在链表中插入一个新节点，使其成为链表的第一个节点，需要进行以下操作：

创建一个新的节点 newNode，并为其分配内存空间。
将新节点的 data 成员设置为 42。
将新节点的 next 指针指向原链表的头节点 head。
将 head 指针指向新节点 newNode，使其成为链表的第一个节点。
因此，正确的操作是：Node* newNode = new Node; newNode->data = 42; newNode->next = head; head = newNode;。
在这个操作中，首先创建一个新的节点 newNode，然后设置 newNode 的 data 值为 42，将 newNode 的 next 指针指向原链表的头部 head，最后将 head 指向新节点 newNode，使其成为链表的第一个节点。
运行以下代码片段的行为是（）
```
int x = 101;
int y = 201;
int *p = &x;
int *q = &y;
p = q;
```
- A. 将 x 的值赋为 201
- B. 将 y 的值赋为 101
- C. 将 q 指向 x 的地址
- D. 将 p 指向 y 的地址

答案：D 、将 p 指向 y 的地址
解析：在这段代码中，首先定义了两个整型变量 x 和 y，分别赋值为 101 和 201。然后定义了两个指针变量 p 和 q，分别指向 x 和 y 的地址。接着将 p 指向 q，即将 p 的值设置为 q 的值，即 p = q，此时 p 和 q 都指向 y 的地址。因此，正确的行为是将 p 指向 y 的地址。

小明在某一天中依次有七个空闲时间段，他想要选出至少一个空闲时间段来练习唱歌，但他希望任意两个练习的时间段之间都有至少两个空闲的时间段让他休息，则小明一共有（）种选择时间段的方案
- A. 31
- B. 18
- C. 21
- D. 33

答案：B 、 18
解析：

1. 这个问题可以用组合数学中的排列组合解决。假设空闲时间段用 O 表示，练习时间段用 X 表示，小明的时间表可以表示为 OOXOOOXOOOXOOOXOOOXOOOXOOOXOOOXOOO。要求任意两个练习时间段之间有至少两个空闲时间段，则可以将问题转化为在剩下的 4 个空闲时间段中选择至少 2 个时间段来插入到 3 个练习时间段之间的问题。
  根据组合数学的知识，从 n 个元素中选择 k 个元素的组合数为 C(n, k) = n! / (k!(n-k)!)。
  在这个问题中，从 4 个空闲时间段中选择 2 个时间段插入到 3 个练习时间段之间，共有 C(4, 2) = 4! / (2! * 2!) = 6 种方式。
  因此，小明一共有 3 个练习时间段的选择方式为 3 种，每种选择方式有 6 种插入空闲时间段的方式，所以小明一共有 3 * 6 = 18 种选择时间段的方案。所以答案是 B. 18。
1. 至少选择一个空闲时间段，且无法选择超过 3 个以上的空闲时间段，所以可以分为三类：
- 选择 1 个空闲时间段，有 7 种选择方式；
- 选择 2 个空闲时间段，有 4 + 3 + 2 + 1 = 10 种选择方式；
- 选择 3 个空闲时间段，有 1 种选择方式。
- 总共有 7 + 10 + 1 = 18 种选择时间段的方案。

组合数学知识

# 组合数学及组合数的定义和使用

组合数学是数学的一个分支，研究有限或可数离散结构的性质、计数、组合和排列问题。它在各种领域如计算机科学、概率论、统计学等中有广泛应用。

组合数（又称二项式系数）表示从一个集合中选取若干个元素的不同方式的数量，而不考虑选取顺序。组合数通常记作

表示从 n 个元素的集合中选取 k 个元素的所有组合数。

# 组合数的定义

组合数

的定义公式为：

其中，n!（n 的阶乘）表示从 1 到 n 的所有正整数的乘积。例如：

# 组合数的使用和概念

# 基本概念

排列：排列考虑选取的顺序，例如从 n 个元素中选取 k 个的排列数表示为
组合：组合不考虑选取的顺序，因此
仅表示从 n 个元素中选取 k 个元素的不同方式，而不考虑顺序。

# 组合数的性质

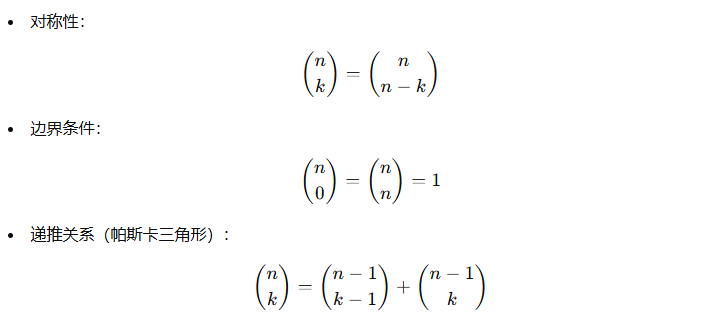
# 组合数的应用

组合数在很多实际问题中有广泛应用，例如：

抽奖和选拔问题：例如从一群人中选取若干人进行抽奖或组成团队。
概率问题：例如计算从一副扑克牌中抽取特定组合的概率。
组合计数问题：例如计算某种方式的分配或安排的数量。

以下关于高精度运算的说法错误的是（）
- A. 高精度计算主要是用来处理大整数或需要保留多位小数的运算
- B. 大整数除以小整数的处理的步骤可以是，将被除数和除数对齐，从左到右逐位尝试将除数乘以某个数，通过减法得到新的被除数，并累加商
- C. 高精度乘法的运算时间只与参与运算的两个整数中长度较长者的位数有关
- D. 高精度加法运算的关键在于逐位相加并处理进位

答案：C 、高精度乘法的运算时间只与参与运算的两个整数中长度较长者的位数有关
解析：实际上，高精度乘法的运算时间与参与运算的两个整数的位数乘积有关，而不仅仅与长度较长者的位数有关。高精度乘法的时间复杂度通常为 O(m*n)，其中 m 和 n 分别为两个整数的位数。因此，高精度乘法的运算时间与两个整数的位数乘积成正比。

链表和数组的区别包括（）
- A. 数组不能排序，链表可以
- B. 链表比数组能存储更多的信息
- C. 数组大小固定，链表大小可动态调整
- D. 以上均正确

答案：C 、数组大小固定，链表大小可动态调整
解析：数组和链表是两种常见的数据结构：

A. 数组和链表都能做排序。比如冒泡排序，里面只有交换相邻元素的操作，这一操作在数组和链表中都可以做。
B. 链表和数组能存储的信息取决于其长度，哪个更长哪个能存储更多信息。
C. 选项是正确的。一旦申请数组，数组的长度就是固定的了。而链表可以申请和释放结点，大小可以动态调整。

数101010(2进制)和166(8进制)的和为（）
- A. 10110000(2进制)
- B. 236(8进制)
- C. 158(10进制)
- D. A0(16进制)

答案：D 、 A0(16进制)
解析：要计算二进制数和八进制数的和，首先将二进制数和八进制数转换为十进制数，然后将其相加，最后将结果转换回对应进制数。
二进制数 101010 转换为十进制数为：12^5 + 02^4 + 12^3 + 02^2 + 12^1 + 02^0 = 32 + 8 + 2 = 42
八进制数 166 转换为十进制数为：18^2 + 68^1 + 6*8^0 = 64 + 48 + 6 = 118
将两个十进制数相加：42 + 118 = 160
对应二进制数为： 10100000(2进制)
对应八进制数为： 240(8进制)
最后将结果 160 转换为十六进制数为： A0(16进制)

以下排序算法的常见实现中，哪个选项的说法是错误的：（）
- A. 冒泡排序算法是稳定的
- B. 简单选择排序是稳定的
- C. 简单插入排序是稳定的
- D. 归并排序算法是稳定的

答案：B 、简单选择排序是稳定的
解析：简单选择排序是不稳定的排序算法。简单选择排序的基本思想是：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。简单选择排序的时间复杂度为 O(n^2)，空间复杂度为 O(1)。

一个字符串中任意个连续的字符组成的子序列称为该字符串的子串，则字符串 abcab 有（）个内容互不相同的子串
- A. 12
- B. 13
- C. 14
- D. 15

答案：A 、 12
解析：

abcab的不相同子串有：
- 长为1的子串：a,b,c
- 长为2的子串：ab,bc,ca
- 长为3的子串：abc,bca,cab
- 长为4的子串：abca,bcab
- 长为5的子串：abcab
- 共有12个。

以下对递归方法的描述中，正确的是：（）
- A. 递归是允许使用多组参数调用函数的编程技术
- B. 递归是通过调用自身来求解问题的编程技术
- C. 递归是面向对象和数据而不是功能和逻辑的编程语言模型
- D. 递归是将用某种高级语言转换为机器代码的编程技术

答案：B 、递归是通过调用自身来求解问题的编程技术
解析：递归是一种编程技术，通过调用自身来解决问题。递归函数在执行时会调用自身，直到满足某个条件才会停止递归。递归函数通常包含两部分：基本情况（base case）和递归情况（recursive case）。基本情况是递归函数停止递归的条件，递归情况是递归函数调用自身的情况。递归函数可以用于解决许多问题，如计算阶乘、斐波那契数列、汉诺塔问题等。

A. 不清楚什么叫“多组参数调用函数”，任意一个带参函数，都可以用多组参数来调用。
C. 面向对象编程（或者说“类”）是面向对象和数据而不是功能和逻辑的编程语言模型。
D. 编译是将用某种高级语言转换为机器代码的编程技术

在计算机中，以下哪个选项描述的数据存储容量最小？（）
- A. 字节（byte）
- B. 比特（bit）
- C. 字（word）
- D. 千字节（kilobyte）

答案：B 、比特（bit）
解析：计算机中的数据存储容量通常使用比特（bit）作为最小的存储单位。比特是计算机中最小的数据单位，表示二进制的 0 或 1。字节（byte）是计算机中常用的存储单位，通常由 8 个比特组成。字（word）是计算机中的一个存储单位，通常表示计算机的一个数据处理单元，字的大小可以根据计算机的架构而变化。千字节（kilobyte）是计算机中的存储容量单位，等于 1024 字节。

一个班级有10个男生和12个女生。如果要选出一个3人的小组，并且小组中必须至少包含1个女生，那么有多少种可能的组合？（）
- A. 1420
- B. 1770
- C. 1540
- D. 2200

答案：A 、 1420
解析：

1. 这个问题可以用组合数学中的排列组合解决。根据题意，小组中至少包含一个女生，最多包含 3 个女生，可以分为三种情况：
- 情况一：小组中有 1 个女生和 2 个男生，共有 C(12, 1) * C(10, 2) = 12 * 45 = 540 种组合。
- 情况二：小组中有 2 个女生和 1 个男生，共有 C(12, 2) * C(10, 1) = 66 * 10 = 660 种组合。
- 情况三：小组中有 3 个女生，共有 C(12, 3) = 220 种组合。
- 总共有 540 + 660 + 220 = 1420 种可能的组合。

代码实现示例

假设我们有一个班级，包含10个男生和12个女生。如果要选出一个3人的小组，并且小组中必须至少包含1个女生，我们可以用组合数来解决。

#include <iostream>

using namespace std;

// 计算阶乘函数
int factorial(int n) {
    int result = 1;
    for (int i = 1; i <= n; ++i) {
        result *= i;
    }
    return result;
}

// 计算组合数函数
int combination(int n, int k) {
    return factorial(n) / (factorial(k) * factorial(n - k));
}

int main() {
    int total_students = 22;
    int males = 10;
    int females = 12;
    int group_size = 3;

    // 计算总的组合数
    int total_combinations = combination(total_students, group_size);

    // 计算全是男生的组合数
    int all_males_combinations = combination(males, group_size);

    // 计算至少包含1个女生的组合数
    int at_least_one_female_combinations = total_combinations - all_males_combinations;

    // 输出结果
    cout << "至少包含1个女生的小组的组合数: " << at_least_one_female_combinations << endl;

    return 0;
}

以下哪个不是操作系统？（）
- A. Linux
- B. Windows
- C. Android
- D. HTML

答案：D 、 HTML
解析：HTML（HyperText Markup Language）是一种用于创建网页的标记语言，不是操作系统。Linux、Windows 和 Android 都是操作系统。操作系统是计算机系统中的核心软件，负责管理计算机的硬件资源、提供用户界面、运行应用程序等功能。Linux 是一种开源的类 Unix 操作系统，Windows 是微软公司开发的操作系统，Android 是谷歌公司开发的移动操作系统。

# 二、阅读程序（判断题正确填√，错误填×；除特殊说明外，判断题1.5分，选择题3分，共计40分）

# 程序1

#include<iostream>
#include<cmath>
using namespace std;

double f(double a,double b,double c){
    double s=(a+b+c)/2;
    return sqrt(s*(s-a)*(s-b)*(s-c));  // sqrt 为求平方根函数  sqrt(4) = 2
}

int main(){
   cout.flags(ios::fixed); //    设置输出格式为固定小数位数
   cout.precision(4); //    设置输出小数位数为4
   
    int a,b,c;
   cin>>a>>b>>c;
   cout<<f(a,b,c)<<endl;
   return 0;
}

解析：本程序较为简洁，最重要的部分是函数 f。阅读f的返回值计算方式可知，这是计算三角形面积的海伦公式，其将 a、b、c 作为浮点数处理，考虑到了三角形面积可能非整数的情形
值得注意：主函数中用到了平时学习较为少见的cout处理方式，其中 cout.flags(ios::fixed) 表示以定点形式显示浮点数,如果没有这一句，则输出会形如 1e4 这样的科学计数法,而 cout.precision(4) 则是指定小数位数为 4 位
这里有一个坑：常用的 setprecision 方法，在输出浮点数时，不会保留尾随 0,而本程序中以上两句的结合，会对 0.1 这样的浮点数,输出 0.1000,其携带尾随 0
最后，本题并没有明确 a、b、c 是否一定能够组成一个三角形。但是根据海伦公式的定义，当 a、b、c 不能组成一个三角形时，其返回值为 0

判断题：
16. （2分）当输入为“2 2 2”时，输出为“1.7321”（）

答案：✅
解析：由输入可知，a=b=c=2，根据海伦公式，s=(2+2+2)/2=3，s-a=s-b=s-c=1，代入公式，得到结果为sqrt(3*1*1*1)=sqrt(3)=1.7321，所以输出为“1.7321”
那么对于我们笔试作答时，我们无法求出sqrt(3)的精确值，所以我们可以直接求1.7321的上下精度加减0.0001，即1.7320和1.7322的平方，来查看是否接近3，如果接近则可以判断为正确

（2分）将第7行中的"（s-b）*（s-c）"改为"（s-c）*（s-b）"不会影响程序运行的结果（）

答案：✅
解析：乘法满足交换律，且即使从程序的角度来考虑，double类型的 s、a、b、c 的计算在输入不超过 1000 时，不会发生溢出。所以 sqrt 开根号的值不变，不会改变程序的运行结果

（2分）程序总是输出四位小数（）

答案：✅
解析：由以上分析，即使结果可以省去末尾的0，也依然会输出为4位小数。实际上这一特性可以由 19、20 两问看出

单选题：

当输入为“3 4 5”时，输出为（）
- A. "6.0000"
- B. "12.0000"
- C. "24.0000"
- D. "30.0000"

答案：A 、 "6.0000"
解析：边长为 3、4、5 的组合是非常典型的直角三角形，3和4是其直角边，因此面积为6，在程序中还要再加上小数点后4位0，所以输出为"6.0000"

当输入为“5 12 13”时，输出为（）
- A. "24.0000"
- B. "30.0000"
- C. "60.0000"
- D. "120.0000"

答案：B 、 "30.0000"
解析：与 19 问类似，5、12、13 也是非常经典的直角三角形三边组合，因此面积再加上小数点后 4 位 0

直角三角形特性回顾：

一个直角三角形的两条直角边的平方和等于斜边的平方，即 a^2 + b^2 = c^2，其中 a 和 b 是直角三角形的两条直角边，c 是斜边
一个直角三角形的面积等于直角边的乘积除以 2，即 S = a * b / 2，其中 a 和 b 是直角三角形的两条直角边，S 是三角形的面积

# 程序2

#include<iostream>
#include<vector>
#include<algorithm> // max函数
using namespace std;

int f(string x,string y){
    int m=x.size();
    int n=y.size();
    vector<vector<int>>v(m+1,vector<int>(n+1,0));
   for(int i=1;i<=m;i++){
       for(int j=1;j<=n;j++){
            if(x[i-1]==y[j-1]){
                v[i][j]=v[i-1][j-1]+1;
            }else{
                v[i][j]=max(v[i-1][j],v[i][j-1]);
            }
        }
    }
    return v[m][n];
}

bool g(string x, string y) {
    if(x.size() != y.size()) {
        return false;
    }
    return f(x + x, y) == y.size();
}

int main(){
    string x,y;
    cin>>x>>y;
    cout<<g(x,y)<<endl;
    return 0;
}

解析：本程序较为简洁，主要是两个函数 f 和 g。f 函数是一个动态规划函数，用于计算两个字符串的最长公共子序列的长度，g 函数是一个判断函数，用于判断两个字符串是否是循环同构的。这段 C++ 程序的目的是判断两个字符串是否为旋转变位词（rotation variant）。换句话说，它检查一个字符串是否可以通过旋转（循环移动）变为另一个字符串

最长公共子序列（LCS，Longest Common Subsequence）

最长公共子序列（LCS，Longest Common Subsequence）是一个经典的计算机科学问题，特别在动态规划中广泛应用。LCS问题描述如下：给定两个字符串，找出它们最长的公共子序列。这里的“子序列”指的是原字符串中按顺序出现但不要求连续的一组字符。

# 定义

给定两个序列 X = {x_1, x_2, ..., x_m} 和 Y = {y_1, y_2, ..., y_n}，找出一个最长的序列 Z = {z_1, z_2, ..., z_k}，使得 Z 同时是 X 和 Y 的子序列。

# 例子

假设有两个字符串：

X = "ABCBDAB"
Y = "BDCAB"

它们的最长公共子序列是 "BCAB" 或者 "BDAB"，长度为 4。

# 动态规划求解方法

LCS 问题可以通过动态规划来高效解决。设 X 和 Y 的长度分别为 m 和 n，我们定义一个二维数组 dp，其中 dp[i][j] 表示 X[0..i-1] 和 Y[0..j-1] 的最长公共子序列的长度。

# 状态转移方程

边界条件:
- 如果 i = 0 或 j = 0，即其中一个字符串为空，则 LCS 长度为 0。所以，初始化 dp[i][0] = 0 和 dp[0][j] = 0。
递推关系:
- 如果 X[i-1] == Y[j-1]，则 dp[i][j] = dp[i-1][j-1] + 1。
- 如果 X[i-1] != Y[j-1]，则 dp[i][j] = max(dp[i-1][j], dp[i][j-1])。

# 算法实现

int LCS(string X, string Y) {
    int m = X.size();
    int n = Y.size();
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));

    for(int i = 1; i <= m; i++) {
        for(int j = 1; j <= n; j++) {
            if(X[i-1] == Y[j-1]) {
                dp[i][j] = dp[i-1][j-1] + 1;
            } else {
                dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
    }
    return dp[m][n];
}

# 时间复杂度和空间复杂度

时间复杂度: 由于要遍历所有 m * n 个状态，时间复杂度为 O(m * n)。
空间复杂度: 使用了一个二维数组存储中间结果，空间复杂度为 O(m * n)。可以通过滚动数组的方式将空间复杂度优化到 O(min(m, n))。

# 应用

LCS 的应用非常广泛，包括但不限于：

文件差异比较：如 diff 工具，用于比较文件内容的变化。
生物信息学：在 DNA 序列比较中，用于找出相似的基因片段。
版本控制系统：如 Git，用于合并分支时检测代码的变化。

头文件与命名空间
```
#include<iostream>
#include<vector>
#include<algorithm> // max函数
using namespace std;
```
- #include<iostream> 包含标准输入输出流的头文件。
- #include<vector> 包含标准库中的向量容器。
- #include<algorithm> 包含标准算法库中的函数，比如 max。
- using namespace std; 使用标准命名空间。

f 函数

int f(string x, string y){
    int m = x.size();
    int n = y.size();
    vector<vector<int>> v(m + 1, vector<int>(n + 1, 0));
    for(int i = 1; i <= m; i++) {
        for(int j = 1; j <= n; j++) {
            if(x[i - 1] == y[j - 1]) {
                v[i][j] = v[i - 1][j - 1] + 1;
            } else {
                v[i][j] = max(v[i - 1][j], v[i][j - 1]);
            }
        }
    }
    return v[m][n];
}

这是一个实现了最长公共子序列（LCS，Longest Common Subsequence）长度的动态规划算法函数。

m 和 n 分别表示字符串 x 和 y 的长度。
v 是一个二维向量，用于存储子问题的解。
双重循环遍历字符串 x 和 y 的每个字符。
如果 x[i - 1] 和 y[j - 1] 相等，则 v[i][j] = v[i - 1][j - 1] + 1，表示当前字符加入到LCS中。
如果不相等，则 v[i][j] = max(v[i - 1][j], v[i][j - 1])，表示当前字符不加入LCS，取之前的最大值。
最后返回 v[m][n]，即 x 和 y 的LCS长度。

g 函数
```
bool g(string x, string y) {
    if(x.size() != y.size()) {
        return false;
    }
    return f(x + x, y) == y.size();
}
```
这个函数用于判断字符串 x 和 y 是否为旋转变位词。
- 首先检查 x 和 y 的长度是否相等，不相等则返回 false。
- 将字符串 x 自身拼接得到 x + x，这样如果 y 是 x 的旋转变位词，它一定是 x + x 的子串。
- 调用 f(x + x, y) 计算 y 是否为 x + x 的最长公共子序列，若长度等于 y.size() 则返回 true，否则返回 false。
main 函数
```
int main(){
    string x, y;
    cin >> x >> y;
    cout << g(x, y) << endl;
    return 0;
}
```
这是程序的入口。
- 从标准输入读取两个字符串 x 和 y。
- 调用 g(x, y) 判断 x 和 y 是否为旋转变位词，并输出结果（1 表示是，0 表示不是）。

判断题：

f 函数的返回值小于等于min(n,m)( ) (注意是假设min(n,m)代码块也处于程序环境中int m=x.size();int n=y.size())

答案：✅
解析：f函数返回两个字符串的最长公共子序列长度，最好情况下，这一公共子序列也只能恰好等于其中某一字符串,其长度不能再超过字符串x和y的最小长度，而 m和n分别代表x和y的长度，故正确

f 函数的返回值等于两个输入字符串的最长公共子串的长度( )

答案：❌
解析：子串与子序列是两个不同的概念，其中子串要求字符必须在原字符串中连续出现，而子序列则只对顺序有要求
例如: ace是abcde的子序列，但不是其子串:cab 既是 abcabc 的子串，又是其子序列。实际上，一个字符串的子串，一定是原串的子序列，但反之不然

当输入两个完全相同的字符串时，g函数的返回值总是true.( )

答案：✅
解析：当两个字符串完全相同时，其旋转变位词也是相同的，因此 g 函数返回 true。例如，输入 "abc" 和 "abc"，它们是旋转变位词，g 函数返回 true。输入的x和y相同时，x + x等于y + y，其和 y 的最长公共子串恰为 y 本身，故 g 函数返回的判断条件成立

单选题：

将第19 行中的“v[m][n]”替换为“v[n][m]”，那么该程序( )
- A. 行为不变
- B. 只会改变输出
- C. 一定非正常退出
- D. 可能非正常退出

答案：D 、可能非正常退出
解析：v[m][n] 表示 x 和 y 的最长公共子序列长度，如果将其替换为 v[n][m]，则表示 y 和 x 的最长公共子序列长度。这样会导致程序的行为发生变化，可能会导致非正常退出。因为在程序中，v 的大小是根据 x 和 y 的长度来确定的，如果将 m 和 n 交换，可能会导致数组越界访问，从而导致非正常退出

当输入为“csp-j p-jcs”时，输出为( )
- A. “0”
- B. “1”
- C. “T”
- D. “F”

答案：B 、 “1”
解析：此时将求 csp-j 和 p-jcs 的最长公共子序列，可知后者恰为前者的子串，故g函数返回的判断条件成立
注意输出的恰为g函数返回的 bool 值，需要排除 T 和 F 两个选项

当输入为“csppsc spsccp”时，输出为( )
- A. “T”
- B. “F”
- C. “0”
- D. “1”

答案：D 、 “1”
解析：此时将求 csppsc 和 spsccp 的最长公共子序列，从前者依次选出第 2、3、5、6、7、9 个字符，恰为 spsccp ，可知后者是前者的子序列，故 g 函数返回的判断条件成立

# 程序3

#include <iostream>
#include <cmath>
using namespace std;

int solve1(int n) {
    return n * n;
}

int solve2(int n) {
    int sum = 0;
    for (int i = 1; i <= sqrt(n); i++) {
        if(n % i == 0) {
            if(n/i == i) {
                sum += i*i;
            } else {
                sum += i*i + (n/i)*(n/i);
           }
        }
    }
    return sum;
}

int main() {
    int n;
    cin >> n;
    cout << solve2(solve1(n)) << " " << solve1(solve2(n)) << endl;
    return 0;
}

解析：本题考察约数。函数solvel返回参数n的平方;数solve2返回参数n的约数的平方和。主函数对两个函数复合调用，先输出n的平方的约数平方和，再输出n的约数平方和的平方

因数（约数）

因数（也称为约数）是指能整除给定整数的整数。换句话说，如果一个整数 a 除以另一个整数 b 后没有余数，那么 b 就是 a 的因数。

# 详细解释

定义：如果 b 是 a 的因数，那么 a \ b 的结果是一个整数，且没有余数。数学上表示为：如果存在整数 c 使得 a = b * c，那么 b 就是 a 的因数。
示例：以数字 12 为例，12 的因数包括：
- 1，因为 12 ÷ 1 = 12（整除）
- 2，因为 12 ÷ 2 = 6（整除）
- 3，因为 12 ÷ 3 = 4（整除）
- 4，因为 12 ÷ 4 = 3（整除）
- 6，因为 12 ÷ 6 = 2（整除）
- 12，因为 12 ÷ 12 = 1（整除）

# 特性

每个正整数至少有两个因数：1 和它本身。例如，7 的因数是 1 和 7。
质数（素数）只有两个因数：1 和它本身。例如，5 是一个质数，它的因数是 1 和 5。
合数有超过两个因数。例如，12 是一个合数，它的因数是 1, 2, 3, 4, 6, 和 12。

# 计算因数的方法

要找到一个数 n 的所有因数，可以遍历从 1 到 \sqrt{n} 的所有整数，并检查它们是否能整除 n。如果 i 是 n 的因数，那么 n / i 也是 n 的因数。

# 示例

#include <iostream>
#include <cmath>
using namespace std;

int main() {
    int n = 12;
    cout << "因数: ";
    for (int i = 1; i <= sqrt(n); i++) {
        if (n % i == 0) {
            cout << i << " ";
            if (i != n / i) {
                cout << n / i << " ";
            }
        }
    }
    cout << endl;
    return 0;
}

输出结果：

因数: 1 12 2 6 3 4

函数solve1：这个函数接受一个整数参数n，返回n的平方。

int solve1(int n) {
    return n * n;
}

函数solve2：这个函数接受一个整数参数n，计算并返回n的所有因数的平方和。具体逻辑如下：
- 先初始化sum为0。
- 遍历从1到sqrt(n)的所有整数i。
- 如果i是n的因数（即n % i == 0），则：
  - 如果n/i等于i，说明这是一个平方因数，只需加一次i*i。
  - 否则，将i*i和(n/i)*(n/i)加到sum中。

int solve2(int n) {
    int sum = 0;
    for (int i = 1; i <= sqrt(n); i++) {
        if(n % i == 0) {
            if(n/i == i) {
                sum += i*i;
            } else {
                sum += i*i + (n/i)*(n/i);
           }
        }
    }
    return sum;
}

主函数main：
- 从标准输入读取一个整数n。
- 计算并输出solve2(solve1(n))和solve1(solve2(n))的结果。

int main() {
    int n;
    cin >> n;
    cout << solve2(solve1(n)) << " " << solve1(solve2(n)) << endl;
    return 0;
}

# 详细步骤

输入n：
- 用户输入一个整数n。
计算solve1(n)：
- 计算并返回n的平方，记作n^2。
计算solve2(solve1(n))：
- 首先计算solve1(n)的结果，即n^2。
- 然后计算并返回n^2所有因数的平方和。
计算solve1(solve2(n))：
- 首先计算solve2(n)的结果，即n的所有因数的平方和。
- 然后计算并返回该和的平方。
输出结果：
- 将solve2(solve1(n))和solve1(solve2(n))的结果打印出来。

# 示例

假设输入n为4，程序的执行过程如下：

solve1(4)返回16。
solve2(16)计算16的所有因数1, 2, 4, 8, 16的平方和，即1 + 4 + 16 + 64 + 256 = 341。
solve2(4)计算4的所有因数1, 2, 4的平方和，即1 + 4 + 16 = 21。
solve1(21)返回21的平方，即441。
输出341 441。

假设输入的n是绝对值不超过1000的整数，完成下面的判断题和单选题:

判断题

如果输入的n为正整数，solve2函数的作用是计算n所有的因子的平方和( )

答案：✅
解析：solve2函数的作用是计算n的所有因数的平方和，即将n的所有因数i的平方i*i相加得到的和

第13-14行的作用是避免n的平方根因子(或n/i)进入第16行而被计算两次( )

答案：✅
解析：if(n/i == i)表示i是n的平方根，即n的因数i只需计算一次，避免重复计算

如果输入的n为质数，solve2(n)的返回值为n^2+1( )

答案：✅
解析：质数的因数只有1和它本身，因此solve2(n)的返回值为1 + n^2，即n^2 + 1

单选题

(4分) 如果输入的n为质数p的平方，那么solve2(n)的返回值为( )
- A. p^2 + p + 1
- B. n^2 + n + 1
- C. n^2 + 1
- D. p^4 + 2p^2 + 1

答案：B 、 n^2 + n + 1
解析：n=p^2 时，它的约数有 1、P、p^2，它们的平方和等于 1+p^2+p^4，再利用 p^2=n 可化为 n^2+n+1

当输入为正整数时，第一项减去第二项的差值一定( )
- A. 大于等于0
- B. 大于等于0且不一定大于0
- C. 小于0
- D. 小于等于0且不一定小于0

答案：D 、小于等于0且不一定小于0
解析：第一项是solve2(solve1(n))，第二项是solve1(solve2(n))，由于solve1和solve2函数的性质，第一项减去第二项的差值可能小于等于0，但不一定小于0

当输入为“5”时，输出为( )
- A. “651 625”
- B. “650 729”
- C. “651 676”
- D. “652 625”

答案：C 、 “651 676”
解析：n = 5，第一项=1+25+625=651、第二项=(1+25)^2=676

# 三、完善程序（单选题，每小题3分，共计30分）

# 程序1（寻找被移除的元素）

问题：原有长度为n+1、公差为1的等差升序数列；将数列输入到程序的数组时移除了一个元素，导致长度为n的升序数组可能不再连续，除非被移除的是第一个或最后一个元素。需要在数组不连续时，找出被移除的元素。试补全程序。

#include <iostream>
#include <vector>

using namespace std;

int find_missing(vector<int>& nums) {
    int left = 0, right = nums.size() - 1;
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == mid + ①) {
            ②
        } else {
            ③
        }
     }
     return ④
}

int main() {
    int n;
    cin >> n;
    vector<int> nums(n);
    for(int i = 0; i < n; i++)cin >> nums[i];
    int missing_number = find_missing(nums);
    if (missing_number == ⑤) {
        cout << "Sequence is consecutive" << endl;
    } else {
        cout << "Missing number is " << missing_number << endl;
    }
    return 0;
}

解析：本题考察二分法。在本程序中find_missing函数就是利用二分法来找到一个长度为n的数组中不连续的位置，从而找出被移除元素的值。只需通过二分找到从左往右第一处使得 nums[i] 不为 nums[0]+i 的的位置，那么在数组中被移除的数就是 nums[0]+i

find_missing函数：
- 接受一个整数向量nums作为输入。
- 使用二分查找法在数组中寻找缺失的数字。
- left和right是二分查找的左右边界。
- mid是中间位置。
- 如果nums[mid] == mid + nums[0]，则说明前半部分没有缺失数字，继续在右半部分查找；否则在左半部分查找。
- 最后返回缺失的数字。
main函数：
- 从标准输入读取数组大小n。
- 读取n个整数到nums向量中。
- 调用find_missing函数查找缺失的数字。
- 如果返回的数字是最后一个数字+1，说明数组是连续的，否则输出缺失的数字。
①处应该填( )
- A. 1
- B. nums[0]
- C. right
- D. left

答案：B 、 nums[0]
解析：若数组连续，一定有 nums[i]==nums[0]+i，所以只需通过二分找到第一处使得 nums[i] 不为 nums[0]+i 的的位置即可。因此二分的判断条件是 nums[mid] == nums[0] + mid

②处应该填( )
- A. left = mid + 1
- B. right = mid – 1
- C. right = mid
- D. left = mid

答案：A 、 left = mid + 1
解析：如果 nums[mid] == mid + nums[0]，说明前半部分没有缺失数字，继续在右半部分查找，所以应该将 left 移动到 mid + 1 的位置

③处应该填( )
- A. left = mid + 1
- B. right = mid – 1
- C. right = mid
- D. left = mid

答案：C 、 right = mid
解析：如果 nums[mid] != mid + nums[0]，说明前半部分有缺失数字，应该在左半部分查找，所以应该将 right 移动到 mid 的位置

④处应该填( )
- A. left = nums[0]
- B. right + nums[0]
- C. mid + nums[0]
- D. right + 1

答案：A 、 left = nums[0]
解析：左端点 left 才能表示最终二分找到的答案(也即不连续位置)，因此最终被移除的数就是 left+nums[0]。首先很容易排除 D，然后因为 mid 只出现在二分的过程中，而且 mid 的定义也在while里，也很容易排除C。可能的问题:这里为何选择A而不选择B，事实上我们二分模板中的书写习惯是return left。在一些情况下return right 会出现问题，但在本题中实际上最后定是 left==right，所以理论上填B也可以

⑤处应该填( )
- A. nums[0] + n
- B. nums[0] + n - 1
- C. nums[0] + n + 1
- D. nums[n-1]

答案：D 、 nums[n-1]
解析：当n个数字连续时，最终我们会得到left=n-1，right=n-1。由 36 所填代码，我们返回的数字就是 nums[0]+n-1 与不连续位置出现在第个数字返回的数值相同。因此我们需要对这两种情况进行讨论，如果n个数字连续，会满足nums[n-1]==nums[0]+n-1，如果是刚好不连续位置在第n个数的话不会使得这个式子成立。因此如果返回数字等于 nums[n-1] 的话，就说明原来n个数连续。故而选择D

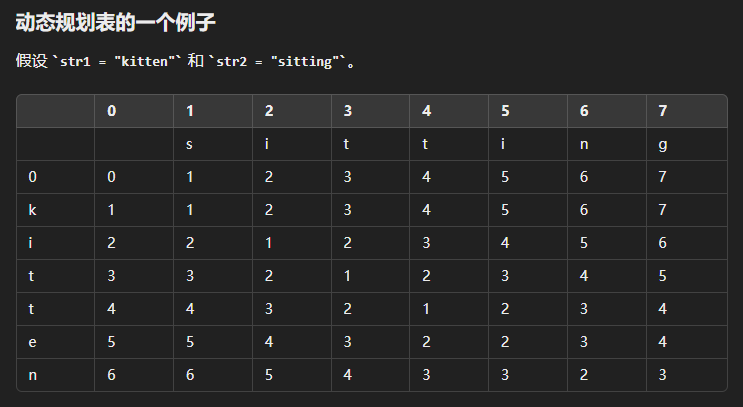
# 程序2（编辑距离）

给定两个字符串，每次操作可以选择删除(Delete)、插入(insert)替换(Replace)个字符，求将第一个字符串转换为第二个字符串所需要的最少操作次数。试补全动态规划算法。

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>  // 引入标准库中的min函数

using namespace std;

// 返回三个数中的最小值
int min(int x, int y, int z) {
    return min(min(x, y), z);  // 使用min来避免无限递归
}

// 动态规划求解编辑距离
int edit_dist_dp(string str1, string str2) {
    int m = str1.length();  // 获取str1的长度
    int n = str2.length();  // 获取str2的长度
    
    // 创建一个二维数组存储子问题的解，大小为 (m+1) x (n+1)
    vector<vector<int>> dp(m + 1, vector<int>(n + 1));

    // 填充dp表格
    for (int i = 0; i <= m; i++) {  // 遍历str1的所有前缀
        for (int j = 0; j <= n; j++) {  // 遍历str2的所有前缀
            if (i == 0) {
                dp[i][j] = j;  // 如果str1为空，编辑距离是插入所有str2的字符
            } else if (j == 0) {
                dp[i][j] = i;  // 如果str2为空，编辑距离是删除所有str1的字符
            } else if (str1[i - 1] == str2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1];  // 当前字符相等，不需要额外操作
            } else {
                dp[i][j] = 1 + min(dp[i][j - 1],    // 插入
                                   dp[i - 1][j],    // 删除
                                   dp[i - 1][j - 1]);  // 替换
            }
        }
    }

    // 返回将str1转换为str2的最小编辑距离
    return dp[m][n];
}

int main() {
    string str1, str2;
    cin >> str1 >> str2;  // 读取两个字符串
    cout << "Minimum number of operations: "  
         << edit_dist_dp(str1, str2) << endl;  // 输出最小编辑距离
    return 0;
}

①处应该填( A )
- A. j
- B. i
- C. m
- D. n
②处应该填( B )
- A. j
- B. i
- C. m
- D. n
③处应该填( A )
- A. str1[i – 1] == str2[j – 1]
- B. str1[i] == str2[j]
- C. str1[i – 1] != str2[j – 1]
- D. str1[i] != str2[j]
④处应该填( B )
- A. dp[i – 1][j – 1] + 1
- B. dp[i – 1][j – 1]
- C. dp[i – 1][j]
- D. dp[i][j – 1]
⑤处应该填( C )
- A. dp[i][j] + 1
- B. dp[i – 1][j – 1] + 1
- C. dp[i – 1][j – 1]
- D. dp[i][j]

真题练习2

讲义

Choose mode

真题考试

真题考试

# 一、单项选择题（共15题，每题2分，共计30分）

# 组合数学及组合数的定义和使用

# 组合数的定义

# 组合数的使用和概念

# 基本概念

# 组合数的性质

# 组合数的应用

# 二、阅读程序（判断题正确填√，错误填×；除特殊说明外，判断题1.5分，选择题3分，共计40分）

# 程序1

# 程序2

# 定义

# 例子

# 动态规划求解方法

# 状态转移方程

# 算法实现

# 时间复杂度和空间复杂度

# 应用

# 程序3

# 详细解释

# 特性

# 计算因数的方法

# 示例

# 详细步骤

# 示例

# 三、完善程序（单选题，每小题3分，共计30分）

# 程序1（寻找被移除的元素）

# 程序2（编辑距离）