2024 csp-j 复赛真题

2024/10/28

# [CSP-J 2024] 扑克牌

# 题目描述

小 P 从同学小 Q 那儿借来一副 $n$ 张牌的扑克牌。

本题中我们不考虑大小王，此时每张牌具有两个属性：花色和点数。花色共有 $4$ 种：方片、草花、红桃和黑桃。点数共有 $13$ 种，从小到大分别为 $A 2 3 4 5 6 7 8 9 T J Q K$ 。注意：点数 $10$ 在本题中记为 $T$ 。

我们称一副扑克牌是完整的，当且仅当对于每一种花色和每一种点数，都恰好有一张牌具有对应的花色和点数。由此，一副完整的扑克牌恰好有 $4 \times 13 = 52$ 张牌。以下图片展示了一副完整的扑克牌里所有的 52 张牌。

小 P 借来的牌可能不是完整的，为此小 P 准备再向同学小 S 借若干张牌。可以认为小 S 每种牌都有无限张，因此小 P 可以任意选择借来的牌。小 P 想知道他至少得向小 S 借多少张牌，才能让从小 S 和小 Q 借来的牌中，可以选出 $52$ 张牌构成一副完整的扑克牌。

为了方便你的输入，我们使用字符 $D$ 代表方片，字符 $C$ 代表草花，字符 $H$ 代表红桃，字符 $S$ 代表黑桃，这样每张牌可以通过一个长度为 $2$ 的字符串表示，其中第一个字符表示这张牌的花色，第二个字符表示这张牌的点数，例如 ${CA}$ 表示草花 $A$ ， ${ST}$ 表示黑桃 $T$ （黑桃 10）。

# 输入格式

输入的第一行包含一个整数 $n$ 表示牌数。

接下来 $n$ 行：

每行包含一个长度为 $2$ 的字符串描述一张牌，其中第一个字符描述其花色，第二个字符描述其点数。

# 输出格式

输出一行一个整数，表示最少还需要向小 S 借几张牌才能凑成一副完整的扑克牌。

# 样例 #1

# 样例输入 #1

1
SA

# 样例输出 #1

# 样例 #2

# 样例输入 #2

4
DQ
H3
DQ
DT

# 样例输出 #2

# 提示

【样例 1 解释】

这一副牌中包含一张黑桃 $A$ ，小 P 还需要借除了黑桃 $A$ 以外的 51 张牌以构成一副完整的扑克牌。

【样例 2 解释】

这一副牌中包含两张方片 $Q$ 、一张方片 $T$ （方片 10）以及一张红桃 3，小 P 还需要借除了红桃 3、方片 $T$ 和方片 $Q$ 以外的 $49$ 张牌。

【样例 3 解释】

见选手目录下的 poker/poker3.in 与 poker/poker3.ans。

这一副扑克牌是完整的，故不需要再借任何牌。

该样例满足所有牌按照点数从小到大依次输入，点数相同时按照方片、草花、红桃、黑桃的顺序依次输入。

【数据范围】

对于所有测试数据，保证： $1 \leq n \leq 52$ ，输入的 $n$ 个字符串每个都代表一张合法的扑克牌，即字符串长度为 $2$ ，且第一个字符为 ${D C H S}$ 中的某个字符，第二个字符为 ${A 2 3 4 5 6 7 8 9 T J Q K}$ 中的某个字符。

测试点编号	$n \leq$	特殊性质
$1$	$1$	A
$2\sim 4$	$52$	A
$5\sim 7$	$52$	B
$8\sim 10$	$52$	无

特殊性质 A：保证输入的 $n$ 张牌两两不同。

特殊性质 B：保证所有牌按照点数从小到大依次输入，点数相同时按照方片、草花、红桃、黑桃的顺序依次输入。

# 解析

我们注意到输入的牌字符串肯定是合法的，那么这题就变成了一个去重问题。

# 两种方法：

# 1. 使用 `std::unique`

std::unique 可以对一个有序的序列去重，并且将重复的放在末尾。具体地，unique 会返回去重后这个序列的末指针。

因此，我们将所有牌用 sort 排序后用一遍 unique 即可。

#include<bits/stdc++.h> // 引入标准库
using namespace std;

const int N=100; // 定义常量 N，表示最大牌数
int n; // 存储输入牌的数量
string s[N]; // 定义字符串数组，用于存储牌

signed main(){
    ios::sync_with_stdio(0); cin.tie(0); // 优化输入输出
    cin >> n; // 读入牌的数量
    for(int i = 1; i <= n; i++) cin >> s[i]; // 读入每张牌
    sort(s + 1, s + n + 1); // 对牌进行排序
    n = unique(s + 1, s + n + 1) - s - 1; // 去重并更新牌的数量
    cout << 52 - n; // 输出剩余牌的数量
    return 0; // 程序结束
}

# 2. 使用 `std::map`

我们可以用内置平衡树的 map 来实现。可以用 map<string,bool> mp 来将一个字符串映射成一个 bool 型，而在代码的最后调用 mp.size() 即可返回有多少张本质不同的卡牌。

#include<bits/stdc++.h> // 引入标准库
using namespace std;

const int N=100; // 定义常量 N，表示最大牌数
int n; // 存储输入牌的数量
string s[N]; // 定义字符串数组，用于存储牌
map<string,bool> mp; // 定义 map，用于存储不同的牌

signed main(){
    ios::sync_with_stdio(0); cin.tie(0); // 优化输入输出
    cin >> n; // 读入牌的数量
    for(int i = 1; i <= n; i++){ // 遍历每张牌
        cin >> s[i]; // 读入牌
        mp[s[i]] = 1; // 将牌映射到 map 中，值为 true
    }
    cout << 52 - mp.size(); // 输出剩余牌的数量
    return 0; // 程序结束
}

# 3. 暴力法

使用一个布尔型二维数组 f[5][20] 来存对应花色是否有此点数，用函数 zhn 转换扑克牌的点数

#include <bits/stdc++.h> // 引入所有标准库
using namespace std;

int n, cnt; // n 为输入的牌数，cnt 用于计数缺失的牌
bool f[5][20]; // 第一维是花色（0-4），第二维是点数（0-19），用于标记牌的存在情况

// 按题意转换点数
int zhn(char x){ 
    if('2' <= x && x <= '9') return x - '0'; // 点数为 2-9，直接返回其整数值
    if(x == 'A') return 1; // A 转换为 1
    if(x == 'T') return 10; // T 转换为 10
    if(x == 'J') return 11; // J 转换为 11
    if(x == 'Q') return 12; // Q 转换为 12
    if(x == 'K') return 13; // K 转换为 13
}

int main(){
    cin >> n; // 读入牌的数量
    for(int i = 1; i <= n; i++){ // 遍历每张牌
        char c1, c2; // c1 为花色，c2 为点数
        cin >> c1 >> c2; // 读入花色和点数
        // 根据花色设置标记
        if(c1 == 'D') f[1][zhn(c2)] = 1; // 方块
        else if(c1 == 'C') f[2][zhn(c2)] = 1; // 梅花
        else if(c1 == 'H') f[3][zhn(c2)] = 1; // 红心
        else if(c1 == 'S') f[4][zhn(c2)] = 1; // 黑桃
    }
    
    /* 遍历扑克牌，检查缺失的牌 */
    for(int i = 1; i <= 4; i++){ // 遍历每种花色
        for(int j = 1; j <= 13; j++){ // 遍历每种点数
            if(!f[i][j]) cnt++; // 如果该牌不存在，计数器加一
        }
    }
    
    cout << cnt; // 输出缺失的牌数
    return 0; // 程序结束
}

# [CSP-J 2024] 地图探险

# 题目描述

小 A 打算前往一片丛林去探险。丛林的地理环境十分复杂，为了防止迷路，他先派遣了一个机器人前去探路。

丛林的地图可以用一个 $n$ 行 $m$ 列的字符表来表示。我们将第 $i$ 行第 $j$ 列的位置的坐标记作 $(i, j)(1 \leq i \leq n, 1 \leq j \leq m)$ 。如果这个位置的字符为 $x$ ，即代表这个位置上有障碍，不可通过。反之，若这个位置的字符为 $.$ ，即代表这个位置是一片空地，可以通过。

这个机器人的状态由位置和朝向两部分组成。其中位置由坐标 $(x, y)(1 \leq x \leq n, 1 \leq y \leq m)$ 刻画，它表示机器人处在地图上第 $x$ 行第 $y$ 列的位置。而朝向用一个 $0 \sim 3$ 的整数 $d$ 表示，其中 $d = 0$ 代表向东， $d = 1$ 代表向南， $d = 2$ 代表向西， $d = 3$ 代表向北。

初始时，机器人的位置为 $(x_0, y_0)$ ，朝向为 $d_0$ 。保证初始时机器人所在的位置为空地。接下来机器人将要进行 $k$ 次操作。每一步，机器人将按照如下的模式操作：

假设机器人当前处在的位置为 $(x, y)$ ，朝向为 $d$ 。则它的方向上的下一步的位置 $(x', y')$ 定义如下：若 $d = 0$ ，则令 $(x', y') = (x, y + 1)$ ；若 $d = 1$ ，则令 $(x', y') = (x + 1, y)$ ；若 $d = 2$ ，则令 $(x', y') = (x, y - 1)$ ；若 $d = 3$ ，则令 $(x', y') = (x - 1, y)$ 。
接下来，机器人判断它下一步的位置是否在地图内，且是否为空地。具体地说，它判断 $(x', y')$ 是否满足 $1 \leq x' \leq n$ ， $1 \leq y' \leq m$ ，且 $(x', y')$ 位置上是空地。如果条件成立，则机器人会向前走一步。它新的位置变为 $(x', y')$ ，且朝向不变。如果条件不成立，则它会执行“向右转”操作。也就是说，令 $d' = (d + 1) mod 4$ （即 $d + 1$ 除以 $4$ 的余数），且它所处的位置保持不变，但朝向由 $d$ 变为 $d'$ 。

小 A 想要知道，在机器人执行完 $k$ 步操作之后，地图上所有被机器人经过的位置（包括起始位置）有几个。

# 输入格式

本题有多组测试数据。

输入的第一行包含一个正整数 $T$ ，表示数据组数。

接下来包含 $T$ 组数据，每组数据的格式如下：

第一行包含三个正整数 $n, m, k$ 。其中 $n, m$ 表示地图的行数和列数， $k$ 表示机器人执行操作的次数。

第二行包含两个正整数 $x_0, y_0$ 和一个非负整数 $d_0$ 。

接下来 $n$ 行，每行包含一个长度为 $m$ 的字符串。保证字符串中只包含 ${x}$ 和 ${.}$ 两个字符。其中，第 $x$ 行的字符串的第 $y$ 个字符代表的位置为 $(x, y)$ 。这个位置是 ${x}$ 即代表它是障碍，否则代表它是空地。数据保证机器人初始时所在的位置为空地。

# 输出格式

对于每组数据：输出一行包含一个正整数，表示地图上所有被机器人经过的位置（包括起始位置）的个数。

# 样例 #1

# 样例输入 #1

2
1 5 4
1 1 2
....x
5 5 20
1 1 0
.....
.xxx.
.x.x.
..xx.
x....

# 样例输出 #1

3
13

# 提示

【样例 1 解释】

该样例包含两组数据。对第一组数据，机器人的状态以如下方式变化：

初始时，机器人位于位置 $(1, 1)$ ，方向朝西（用数字 $2$ 代表）。
第一步，机器人发现它下一步的位置 $(1, 0)$ 不在地图内，因此，它会执行“向右转”操作。此时，它的位置仍然为 $(1, 1)$ ，但方向朝北（用数字 $3$ 代表）。
第二步，机器人发现它下一步的位置 $(0, 1)$ 不在地图内，因此，它仍然会执行“向右转”操作。此时，它的位置仍然为 $(1, 1)$ ，但方向朝东（用数字 $0$ 代表）。
第三步，机器人发现它下一步的位置 $(1, 2)$ 在地图内，且为空地。因此，它会向东走一步。此时，它的位置变为 $(1, 2)$ ，方向仍然朝东。
第四步，机器人发现它下一步的位置 $(1, 3)$ 在地图内，且为空地。因此，它会向东走一步。此时，它的位置变为 $(1, 3)$ ，方向仍然朝东。

因此，四步之后，机器人经过的位置有三个，分别为 $(1, 1),(1, 2),(1, 3)$ 。

对第二组数据，机器人依次执行的操作指令为：向东走到 $(1, 2)$ ，向东走到 $(1, 3)$ ，向东走到 $(1, 4)$ ，向东走到 $(1, 5)$ ，向右转，向南走到 $(2, 5)$ ，向南走到 $(3, 5)$ ，向南走到 $(4, 5)$ ，向南走到 $(5, 5)$ ，向右转，向西走到 $(5, 4)$ ，向西走到 $(5, 3)$ ，向西走到 $(5, 2)$ ，向右转，向北走到 $(4, 2)$ ，向右转，向右转，向南走到 $(5, 2)$ ，向右转，向右转。

【样例 2】

见选手目录下的 explore/explore2.in 与 explore/explore2.ans。

该样例满足第 $3\sim 4$ 个测试点的限制条件。

【样例 3】

见选手目录下的 explore/explore3.in 与 explore/explore3.ans。

该样例满足第 $5$ 个测试点的限制条件。

【样例 4】

见选手目录下的 explore/explore4.in 与 explore/explore4.ans。

该样例满足第 $6$ 个测试点的限制条件。

【样例 5】

见选手目录下的 explore/explore5.in 与 explore/explore5.ans。

该样例满足第 $8 \sim 10$ 个测试点的限制条件。

【数据范围】

对于所有测试数据，保证： $1 \leq T \leq 5, 1 \leq n, m \leq 10^3$ ， $1 \leq k \leq 10^6$ ， $1 \leq x_0 \leq n$ ， $1 \leq y_0 \leq m$ ， $0 \leq d_0 \leq 3$ ，且机器人的起始位置为空地。

测试点编号	$n$	$m$	$k$	特殊性质
$1$	$=1$	$\leq 2$	$=1$	无
$2$	$=1$	$\leq 2$	$=1$	无
$3$	$\leq 10^2$	$\leq 10^2$	$=1$	无
$4$	$\leq 10^2$	$\leq 10^2$	$=1$	无
$5$	$=1$	$\leq 10^3$	$\leq 2\times 10^3$	地图上所有位置均为空地
$6$	$=1$	$\leq 10^3$	$\leq 2\times 10^3$	无
$7$	$\leq 10^3$	$\leq 10^3$	$\leq 10^6$	地图上所有位置均为空地
$8$	$\leq 10^3$	$\leq 10^3$	$\leq 10^6$	无
$9$	$\leq 10^3$	$\leq 10^3$	$\leq 10^6$	无
$10$	$\leq 10^3$	$\leq 10^3$	$\leq 10^6$	无

# 解析

经典模拟题，对于模拟题，如果没有简单思路，直接暴力实现题目要求即可

题目背景
本题属于模拟题，为了解释清楚题意，题目长度偏长，放在这个位置可能对于年龄较低的参赛选手不太友好。

模拟要点

在代码中可以设置两个位移数组：
```
const int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};
```
以简便地完成转向的移动。
注意横纵坐标的使用，尤其是变量名（如 y1）不应定义为全局变量，以免出现编译错误。
使用错误的横纵坐标可能导致通过样例但未通过评测的情况（例如将 y1 错写为 y0）。
多测时请不要清空数据，爆零两行泪。

参考代码

#include <bits/stdc++.h>  // 包含所有标准库
using namespace std;

bool vis[1005][1005];  // 访问标记数组，记录每个位置是否被访问过
char ch[1005][1005];   // 存储地图的字符数组
const int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};  // 位移数组，用于控制方向（右、下、左、上）

void solve() {
    int n, m, k, x0, y0, d0;  // n: 行数, m: 列数, k: 移动步数, x0: 当前行, y0: 当前列, d0: 当前方向
    memset(vis, 0, sizeof(vis));  // 初始化访问数组为false
    cin >> n >> m >> k;  // 输入行数、列数和移动步数
    cin >> x0 >> y0 >> d0;  // 输入起始位置（x0, y0）和初始方向（d0）

    // 读取地图数据
    for (int i = 1; i <= n; i++) {
        char s[1005];  // 每一行的字符数组
        cin >> s;  // 输入一行地图
        for (int j = 1; j <= m; j++)
            ch[i][j] = s[j - 1];  // 将字符存入地图数组
    }

    vis[x0][y0] = true;  // 标记起始位置为已访问

    // 进行 k 步移动
    for (int i = 1; i <= k; i++) {
        int x1 = x0 + dx[d0], y1 = y0 + dy[d0];  // 计算下一个位置
        // 检查下一个位置是否合法且未被障碍物阻挡
        if (1 <= x1 && x1 <= n && 1 <= y1 && y1 <= m && ch[x1][y1] == '.') {
            x0 = x1;  // 更新当前位置
            y0 = y1;
        } else {
            d0 = (d0 + 1) % 4;  // 如果无法移动，顺时针转向
        }
        vis[x0][y0] = true;  // 标记当前位置为已访问
    }

    int ans = 0;  // 计数已访问的位置数量
    // 统计已访问的位置
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++)
            ans += vis[i][j];  // 累加已访问的数量
    }
    cout << ans << endl;  // 输出结果
}

int main() {
    int T;  // 测试用例数量
    cin >> T;  // 输入测试用例数量
    while (T--) {
        solve();  // 处理每个测试用例
    }
}

# [CSP-J 2024] 小木棍

# 题目描述

小 S 喜欢收集小木棍。在收集了 $n$ 根长度相等的小木棍之后，他闲来无事，便用它们拼起了数字。用小木棍拼每种数字的方法如下图所示。

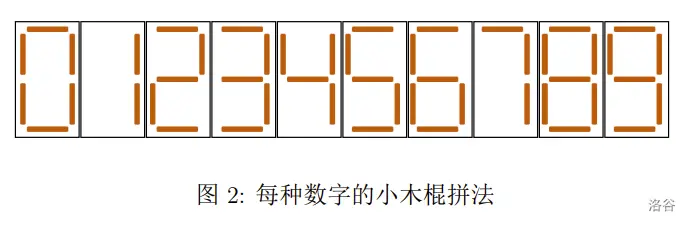
现在小 S 希望拼出一个正整数，满足如下条件：

拼出这个数恰好使用 $n$ 根小木棍；
拼出的数没有前导 $0$ ；
在满足以上两个条件的前提下，这个数尽可能小。

小 S 想知道这个数是多少，可 $n$ 很大，把木棍整理清楚就把小 S 折腾坏了，所以你需要帮他解决这个问题。如果不存在正整数满足以上条件，你需要输出 $-1$ 进行报告。

# 输入格式

本题有多组测试数据。

输入的第一行包含一个正整数 $T$ ，表示数据组数。

接下来包含 $T$ 组数据，每组数据的格式如下：

一行包含一个整数 $n$ ，表示木棍数。

# 输出格式

对于每组数据：输出一行，如果存在满足题意的正整数，输出这个数；否则输出 $-1$ 。

# 样例 #1

# 样例输入 #1

# 样例输出 #1

# 提示

【样例 1 解释】

对于第一组测试数据，不存在任何一个正整数可以使用恰好一根小木棍摆出，故输出 $-1$ 。
对于第四组测试数据，注意 $0$ 并不是一个满足要求的方案。摆出 $9$ 、 $41$ 以及 $111$ 都恰好需要 $6$ 根小木棍，但它们不是摆出的数最小的方案。
对于第五组测试数据，摆出 $208$ 需要 $5 + 6 + 7 = 18$ 根小木棍。可以证明摆出任何一个小于 $208$ 的正整数需要的小木棍数都不是 $18$ 。注意尽管拼出 $006$ 也需要 $18$ 根小木棍，但因为这个数有前导零，因此并不是一个满足要求的方案。

【数据范围】

对于所有测试数据，保证： $1 \leq T \leq 50$ ， $1 \leq n \leq 10^5$ 。

测试点编号	$n\leq$	特殊性质
$1$	$20$	无
$2$	$50$	无
$3$	$10^3$	A
$4,5$	$10^5$	A
$6$	$10^3$	B
$7,8$	$10^5$	B
$9$	$10^3$	无
$10$	$10^5$	无

特殊性质 A：保证 $n$ 是 $7$ 的倍数且 $n \geq 100$ 。

特殊性质 B：保证存在整数 $k$ 使得 $n = 7k + 1$ ，且 $n \geq 100$ 。

# 解析

# 题意概括

给定一个自然数 $N$ ，要求用 $N$ 根木棍摆出最小的数字（不含前导 0）。

# 思路

可以通过分类讨论并考虑 N \mod 7 的余数来解决问题：

余数为 0：答案为 $\frac{N}{7}$ 个 8。
余数为 1：
- 特判： $N = 1$ 时无答案，输出 -1。
- 其他情况：答案为 10 拼接 $\frac{(N-8)}{7}$ 个 8。
余数为 2：答案为 1 和 $\frac{(N-2)}{7}$ 个 8。
余数为 3：
- 特判： $N = 3$ 时答案为 7。
- 特判： $N = 10$ 时答案为 22。
- 其他情况：答案为 200 拼接 $\frac{(N-17)}{7}$ 个 8。
余数为 4：
- 特判： $N = 4$ 时答案为 4。
- 其他情况：答案为 20 拼接 $\frac{(N-11)}{7}$ 个 8。
余数为 5：答案为 2 拼接 $\frac{(N-5)}{7}$ 个 8。
余数为 6：答案为 6 拼接 $\frac{(N-6)}{7}$ 个 8。

# 代码

#include<bits/stdc++.h>  // 引入头文件
using namespace std;    // 使用标准命名空间

long long n, t, ans, stick[10] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6}; // 声明变量

int main() {  // 主函数
    cin >> t;  // 输入测试用例数量
    while (t--) {  // 遍历每个测试用例
        cin >> n;  // 输入自然数 N
        ans = 1e9 + 1;  // 初始化答案为一个很大的数
        if (n == 1) cout << -1;  // 特判：N=1时无答案
        else if (n == 2) cout << 1;  // 特判：N=2时答案为1
        else if (n == 3) cout << 7;  // 特判：N=3时答案为7
        else if (n == 4) cout << 4;  // 特判：N=4时答案为4
        else if (n == 5) cout << 2;  // 特判：N=5时答案为2
        else if (n == 6) cout << 6;  // 特判：N=6时答案为6
        else if (n == 7) cout << 8;  // 特判：N=7时答案为8
        else if (n % 7 == 0) {  // 余数为0的情况
            for (int i = 1; i <= n / 7; i++) cout << 8;  // 输出 N/7 个 8
        }
        else if (n % 7 == 1) {  // 余数为1的情况
            cout << 10;  // 输出10
            for (int i = 1; i <= (n - 8) / 7; i++) cout << 8;  // 输出 (N-8)/7 个 8
        }
        else if (n % 7 == 2) {  // 余数为2的情况
            cout << 1;  // 输出1
            for (int i = 1; i <= (n - 2) / 7; i++) cout << 8;  // 输出 (N-2)/7 个 8
        }
        else if (n % 7 == 3) {  // 余数为3的情况
            if (n == 10) cout << 22;  // 特判：N=10时答案为22
            else {
                cout << 200;  // 输出200
                for (int i = 1; i <= (n - 17) / 7; i++) cout << 8;  // 输出 (N-17)/7 个 8
            }
        }
        else if (n % 7 == 4) {  // 余数为4的情况
            cout << 20;  // 输出20
            for (int i = 1; i <= (n - 11) / 7; i++) cout << 8;  // 输出 (N-11)/7 个 8
        }
        else if (n % 7 == 5) {  // 余数为5的情况
            cout << 2;  // 输出2
            for (int i = 1; i <= (n - 5) / 7; i++) cout << 8;  // 输出 (N-5)/7 个 8
        }
        else if (n % 7 == 6) {  // 余数为6的情况
            cout << 6;  // 输出6
            for (int i = 1; i <= (n - 6) / 7; i++) cout << 8;  // 输出 (N-6)/7 个 8
        }
        cout << "\n";  // 输出换行
    }
    return 0;  // 返回0表示程序正常结束
}

# [CSP-J 2024] 接龙

# 题目描述

在玩惯了成语接龙之后，小 J 和他的朋友们发明了一个新的接龙规则。

总共有 $n$ 个人参与这个接龙游戏，第 $i$ 个人会获得一个整数序列 $S_i$ 作为他的词库。

一次游戏分为若干轮，每一轮规则如下：

$n$ 个人中的某个人 $p$ 带着他的词库 $S_p$ 进行接龙。若这不是游戏的第一轮，那么这一轮进行接龙的人不能与上一轮相同，但可以与上上轮或更往前的轮相同。
接龙的人选择一个长度在 $[2, k]$ $[2, k]$ 的 $S_p$ $S p $ 的连续子序列 $A$ $A$ 作为这一轮的接龙序列，其中 $k$ $k$ 是给定的常数。若这是游戏的第一轮，那么 $A$ $A$ 需要以元素 $1$ $1$ 开头，否则 $A$ $A$ 需要以上一轮的接龙序列的最后一个元素开头。
- 序列 $A$ 是序列 $S$ 的连续子序列当且仅当可以通过删除 $S$ 的开头和结尾的若干元素（可以不删除）得到 $A$ 。

为了强调合作，小 J 给了 $n$ 个参与游戏的人 $q$ 个任务，第 $j$ 个任务需要这 $n$ 个人进行一次游戏，在这次游戏里进行恰好 $r_j$ 轮接龙，且最后一轮的接龙序列的最后一个元素恰好为 $c_j$ 。为了保证任务的可行性，小 J 请来你判断这 $q$ 个任务是否可以完成的，即是否存在一个可能的游戏过程满足任务条件。

# 输入格式

本题有多组测试数据。

输入的第一行包含一个正整数 $T$ ，表示数据组数。

接下来包含 $T$ 组数据，每组数据的格式如下：

第一行包含三个整数 $n, k, q$ ，分别表示参与游戏的人数、接龙序列长度上限以及任务个数。

接下来 $n$ 行：

第 $i$ 行包含 $(l_i + 1)$ 个整数 $l_i, S_{i,1}, S_{i,2}, ..., S_{i,l_i}$ ，其中第一个整数 $l_i$ 表示序列 $S_i$ 的长度，接下来 $l_i$ 个整数描述序列 $S_i$ 。

接下来 $q$ 行：

第 $j$ 行包含两个整数 $r_j, c_j$ ，描述一个任务。

# 输出格式

对于每个任务：输出一行包含一个整数，若任务可以完成输出 1，否则输出 0。

# 样例 #1

# 样例输入 #1

1
3 3 7
5 1 2 3 4 1
3 1 2 5
3 5 1 6
1 2
1 4
2 4
3 4
6 6
1 1
7 7

# 样例输出 #1

# 提示

【样例 1 解释】

在下文中，我们使用 $\{A_i\} = \{A_1, A_2, ... , A_r\}$ 表示一轮游戏中所有的接龙序列， $\{p_i\} = \{p_1, p_2, ... , p_r\}$ 表示对应的接龙的人的编号。由于所有字符均为一位数字，为了方便我们直接使用数字字符串表示序列。

对于第一组询问， $p_1 = 1$ 、 $A_1 = 12$ 是一个满足条件的游戏过程。
对于第二组询问，可以证明任务不可完成。注意 $p_1 = 1$ 、 $A_1 = 1234$ 不是合法的游戏过程，因为此时 $|A_1| = 4 > k$ 。
对于第三组询问， $\{p_i\} = \{2, 1\}$ 、 $\{A_i\} = \{12, 234\}$ 是一个满足条件的游戏过程。
对于第四组询问，可以证明任务不可完成。注意 $\{p_i\} = \{2, 1, 1\},\{A_i\} = \{12, 23, 34\}$ 不是一个合法的游戏过程，因为尽管所有的接龙序列长度均不超过 $k$ ，但第二轮和第三轮由同一个人接龙，不符合要求。
对于第五组询问， $\{p_i\} = \{1, 2, 3, 1, 2, 3\}$ 、 $\{A_i\} = \{12, 25, 51, 12, 25, 516\}$ 是一个满足条件的游戏过程。
对于第六组询问，可以证明任务不可完成。注意每个接龙序列的长度必须大于等于 $2$ ，因此 $A_1 = 1$ 不是一个合法的游戏过程。
对于第七组询问，所有人的词库均不存在字符 $7$ ，因此任务显然不可完成。

【样例 2】

见选手目录下的 chain/chain2.in 与 chain/chain2.ans。

该样例满足测试点 1 的特殊性质。

【样例 3】

见选手目录下的 chain/chain3.in 与 chain/chain3.ans。

该样例满足测试点 2 的特殊性质。

【样例 4】

见选手目录下的 chain/chain4.in 与 chain/chain4.ans。

该样例满足特殊性质 A，其中前两组测试数据满足 $n \leq 1000$ 、 $r \leq 10$ 、单组测试数据内所有词库的长度和 $\leq 2000$ 、 $q \leq 1000$ 。

【样例 5】

见选手目录下的 chain/chain5.in 与 chain/chain5.ans。

该样例满足特殊性质 B，其中前两组测试数据满足 $n \leq 1000$ 、 $r \leq 10$ 、单组测试数据内所有词库的长度和 $\leq 2000$ 、 $q \leq 1000$ 。

【样例 6】

见选手目录下的 chain/chain6.in 与 chain/chain6.ans。

该样例满足特殊性质 C，其中前两组测试数据满足 $n \leq 1000$ 、 $r \leq 10$ 、单组测试数据内所有词库的长度和 $\leq 2000$ 、 $q \leq 1000$ 。

【数据范围】

对于所有测试数据，保证：

$1 \leq T \leq 5$ ；
$1 \leq n \leq 10^5$ ， $2 \leq k \leq 2 \times 10^5$ ， $1 \leq q \leq 10^5$ ；
$1 \leq l_i \leq 2 \times 10^5$ ， $1 \leq S_{i,j} \leq 2 \times 10^5$ ；
$1 \leq r_j \leq 10^2$ ， $1 \leq c_j \leq 2 \times 10^5$ ；
设 $\sum l$ 为单组测试数据内所有 $l_i$ 的和，则 $\sum l\leq 2\times 10^5$ 。

测试点	$n\leq$	$r\leq$	$\sum l\leq$	$q\leq$	特殊性质
$1$	$10^3$	$1$	$2000$	$10^3$	无
$2,3$	$10$	$5$	$20$	$10^2$	无
$4,5$	$10^3$	$10$	$2000$	$10^3$	A
$6$	$10^5$	$10^2$	$2\times 10^5$	$10^5$	A
$7,8$	$10^3$	$10$	$2000$	$10^3$	B
$9,10$	$10^5$	$10^2$	$2\times 10^5$	$10^5$	B
$11,12$	$10^3$	$10$	$2000$	$10^3$	C
$13,14$	$10^5$	$10^2$	$2\times 10^5$	$10^5$	C
$15\sim 17$	$10^3$	$10$	$2000$	$10^3$	无
$18\sim 20$	$10^5$	$10^2$	$2\times 10^5$	$10^5$	无

特殊性质 A：保证 $k = 2 \times 10^5$ 。

特殊性质 B：保证 k ≤ 5。

特殊性质 C：保证在单组测试数据中，任意一个字符在词库中出现次数之和均不超过 $5$ 。

# 解析

这是一道 CSP-S 第 1.5 题难度的动态规划，但是放在 CSP-J 来考严格来说也没有超纲。

问题描述：
- S 由所有人的拥有的序列首尾相接而成。
- 元素 S[j] 属于第 person[j] 个人。
- 第 i 个人与第 i+1 个人拥有的序列在 S 中的分界线为 end[i]。
数据结构：
- head[round][j] 表示第 round 轮以元素 S[j] 开头是否可行。
- tail[round][j] 表示第 round 轮以元素 S[j] 结尾是否可行。
- headSum 是第 round 轮中 head[round] 的左闭右开前缀和。
- owner[round][x]:
  - 为 0 表示第 round 轮没有人能以值为 x 的元素结尾。
  - 为正整数表示第 round 轮第 owner[round][x] 个人能以值为 x 的元素结尾。
  - 为正无穷表示第 round 轮有超过一个人能以值为 x 的元素结尾。

#include <iostream> // 引入输入输出流库
#include <climits>  // 引入限制常量库
#include <algorithm> // 引入算法库

namespace noip { // 定义命名空间 noip
    typedef long long Int; // 定义长整型别名 Int

    constexpr Int maxN = 100'000; // 定义最大人数
    constexpr Int maxR = 100; // 定义最大轮数
    constexpr Int maxLSum = 200'000; // 定义最大序列长度
    constexpr Int maxS = 200'000; // 定义最大元素值
    constexpr Int veryBeginningS = 1; // 定义序列开始元素的值

    Int S[maxLSum], person[maxLSum]; // 定义序列和每个元素所属的人
    bool tail[1+maxR][maxLSum], head[1+maxR][maxLSum]; // 定义头尾可行性数组
    Int owner[1+maxR][1+maxS]; // 定义每轮中每个元素的拥有者
    Int n, k, q; // 定义人数、序列长度、查询次数
    Int l[1+maxN], end[1+maxN]; // 定义每个人的序列长度和序列的结束索引

    void main() { // 主函数
        std::cin >> n >> k >> q; // 输入人数、序列长度、查询次数
        end[0] = 0; // 初始化序列结束索引
        for (Int i = 1; i <= n; i++) { // 遍历每个人
            end[i] = end[i-1]; // 更新当前人的结束索引
            std::cin >> l[i]; // 输入当前人的序列长度
            for (Int j = 1; j <= l[i]; j++) std::cin >> S[end[i]++]; // 输入当前人的序列元素
            for (Int j = end[i-1]; j < end[i]; j++) person[j] = i; // 记录每个元素所属的人
        }
        for (Int round = 1; round <= maxR; round++) { // 遍历每一轮
            if (round > 1) // 如果不是第一轮
                for (Int j = 0; j < end[n]; j++) head[round][j] = // 更新头可行性
                    owner[round-1][S[j]] == LLONG_MAX ? true : // 如果上轮是无穷大，表示可行
                    owner[round-1][S[j]] == 0 ? false : // 如果上轮是0，表示不可行
                    owner[round-1][S[j]] != person[j]; // 否则根据所属人判断可行性
            else // 如果是第一轮
                for (Int j = 0; j < end[n]; j++)
                    head[round][j] = S[j] == veryBeginningS; // 仅当元素是起始元素时可行

            static Int headSum[1+maxLSum+1]; // 定义头前缀和数组
            headSum[0] = 0; // 初始化前缀和
            for (Int j = 0; j < end[n]; j++) headSum[j+1] = headSum[j] + head[round][j]; // 计算前缀和

            for (Int right = 0; right < end[n]; right++) { // 遍历序列元素
                Int left = std::max(end[person[right]-1], right-k+1); // 计算左边界
                tail[round][right] = headSum[right] - headSum[left]; // 更新尾可行性
            }

            std::fill(owner[round]+1, owner[round]+1+maxS, 0); // 初始化拥有者数组
            for (Int j = 0; j < end[n]; j++) if (tail[round][j]) owner[round][S[j]] = // 更新拥有者
                owner[round][S[j]] == 0 ? person[j] : // 如果之前没有人，记录当前人
                owner[round][S[j]] == person[j] ? person[j] : // 如果是同一个人，保持不变
                LLONG_MAX; // 否则标记为无穷大
        }
        while (q--) { // 处理查询
            Int r, c; std::cin >> r >> c; // 输入查询的轮次和元素值
            std::cout << (Int)bool(owner[r][c]) << std::endl; // 输出结果
        }
    }
}

int main() { // 主入口函数
    noip::Int T; std::cin >> T; // 输入测试案例数
    while (T--) noip::main(); // 处理每个测试案例
    return 0; // 返回0，表示程序正常结束
}

复赛注意事项

讲义