真题练习

CSP-J 2019 入门级 第一轮 选择题

1. 中国的国家顶级域名是（）

• A. .cn
• B. .ch
• C. .chn
• D. .china

答案：A
解析：国家顶级域名为.cn（中国）、.us（美国）、.uk（英国）等。

---

2. 二进制数11 1011 1001 0111和 01 0110 1110 1011 进行逻辑与运算的结果是（）

• A. 01 0010 1000 1011
• B. 01 0010 1000 0001
• C. 01 0010 1000 0011
• D. 01 0010 1001 0011

答案：C
解析：逻辑与运算，两个数对应位都为1时结果为1，否则为0。

---

3. 一个32位整型变量占用（）字节。

• A. 32
• B. 4
• C. 128
• D. 8

答案：B
解析：

• 一个32位整型变量占用 4字节 (Bytes)：

1. 位与字节的换算：

   • 1字节 = 8位 (bit)。
   • 32位表示这个变量由32个二进制位组成。
   • 因此，32位 ÷ 8位/字节 = 4字节。

2. 整型变量的定义：

   • 32位系统或编译器中，int 类型的整型变量通常是32位的，因此占用4字节。
   • 这个长度决定了它可以存储的整数范围。对于有符号整型（signed int），范围是从 -2^31 到 2^31 - 1；对于无符号整型（unsigned int），范围是从 0 到 2^32 - 1。

• 为什么是32位：
  • 在大多数现代编译器（尤其是32位系统上），int 类型的默认大小为32位。
  • 这种设计通常是为了平衡内存使用和处理能力。

---

4. 程序段如下：

s = a;
for (b = 1; b <= c; b++) s = s - 1;

上述程序段的最终值是（）

• A. s = a - c
• B. s = a - b
• C. s = s - c
• D. s = b - c

答案：A
解析：

1. 初始状态：

   • s = a;：首先，s 被赋值为 a，这意味着 s 开始时与 a 的值相同。

2. 第一次循环 (b = 1)：

   • s = s - 1;：此时，s 的值是 a，所以这一步后 s 变成 a - 1。

3. 第二次循环 (b = 2)：

   • 现在 s 的值已经变为 a - 1，所以 s = s - 1; 这一步后，s 的值变为 (a - 1) - 1，也就是 a - 2。

4. 第三次循环 (b = 3)：

   • 现在 s 的值是 a - 2，执行 s = s - 1; 后，s 变为 a - 3。

5. 继续循环：

   • 每次循环都会让 s 的值减去 1，而 s 的值是基于上一次循环的结果。

6. 循环结束时：

   • 经过 c 次循环后，s 最终减少了 c 次，所以最终 s = a - c。

• 重要点：
  • 由于 s = s - 1; 使用的是当前的 s，因此每次递减的基础是上一次递减后的 s，而不是重新从 a 开始。
  • a 的值在整个过程中保持不变，s 的值在每次循环中基于之前的 s 减 1。
  • 程序的最终值是 s = a - c，因为 s 一开始是 a，然后在循环中每次减去 1，共减了 c 次。
  • 正确答案是 A. s = a - c。

---

5. 有100个已排序的数据元素，采用折半查找时，最大比较次数为（）

• A. 7
• B. 10
• C. 6
• D. 8

答案：A
解析：

• 折半查找（也叫二分查找）的时间复杂度是 O(log₂n)，其中 n 是数据元素的个数。折半查找的过程是每次将搜索范围减半，直到找到目标元素或者搜索范围为空。

• 对于这道题目，已知有 100 个已排序的数据元素，我们需要找到最大比较次数，也就是最坏情况下要进行多少次比较。

• 计算过程：

  • 每次比较后，剩余的搜索元素是前一次的一半。搜索次数的最大值等于让元素个数减少到 1 所需的次数。
  • 公式为：log₂n，其中 n 是元素个数。

  计算 log₂(100)：

  • $\log_2(100) \approx 6.64$

  由于比较次数必须是整数，所以向上取整，得到 7 次。

• 在最坏情况下，折半查找 100 个元素时，最多需要比较 7 次。

因此，正确答案是 A. 7。

---

6. 链表不具备的特性是（）

• A. 插入删除不需移动元素
• B. 不必先计算存储空间
• C. 存储结构是线性表
• D. 可随机访问任意元素

答案：D
解析：链表通过指针访问元素，无法随机访问，而需要从头节点开始遍历。

---

7. 把8个同样的球放在5个同样的袋子里，允许有的袋子空着不放，问共有多少种不同的分法?( )

提示:如果8个球都放在一个袋子里，无论是哪个袋子，都只算同一种分法

• A. 22
• B. 24
• C. 18
• D. 20

答案：C
解析：枚举法求解，8个同样的球分1个袋子共1种方案，分2个袋子共4种方案，分3个袋子共5种方案，分4个袋子共5种方案，分5个袋子共3种方案，合计18种

---

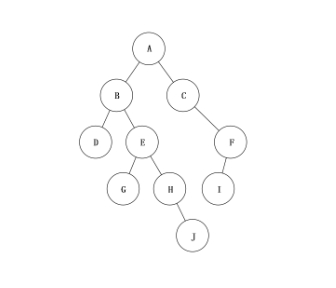
8. 一棵二叉树如图所示，若采用顺序存储结构，即用一维数组元素存储该二叉树中的结点(根结点的下标为1，若某结点的下标为i，则其左孩子位于下标2i处、右孩子位于下标 2i+1处)，则该数组的最大下标至少为( )

• A. 15
• B. 12
• C. 10
• D. 6

答案：A
解析：根据题目给定的规则可知，下标最大的结点为树中深度最大且最靠右的结点,其下标为((1*2+1)*2+1)*2+1=15

---

9. 100以内最大的素数是（）

• A. 89
• B. 97
• C. 91
• D. 93

答案：B
解析：100以内最大的素数是97。 素数是指只能被1和它本身整除的自然数。为了找出100以内最大的素数，我们可以从100往下找，依次验证数字是否为素数。

从100开始，依次检查：

• 100不是素数，因为它可以被2和5整除。
• 99不是素数，因为它可以被3整除。
• 98不是素数，因为它可以被2整除。
• 97是素数，因为它只能被1和97整除。

所以，100以内最大的素数是97。

验证素数的步骤一般是检查该数能否被小于或等于其平方根的所有素数整除。如果不能被整除，则该数是素数。

---

10. 319 和 377 的最大公约数是（）

• A. 27
• B. 33
• C. 29
• D. 31

答案：C
解析：

• 使用辗转相除法得到 GCD(319, 377) = 29
• 计算方法可以使用辗转相除法（欧几里得算法），步骤如下：

1. 用较大的数377除以较小的数319，得到商1和余数58：

   377\div319 = 1\text{ 余 }58

2. 用319除以58，得到商5和余数29：

   319\div58 = 5\text{ 余 }29

3. 用58除以29，得到商2且余数为0：

   58\div29 = 2\text{ 余 }0

4. 当余数为0时，最后一个非零余数就是最大公约数，所以319和377的最大公约数是29。

---

11. 新学期开学了，小胖想减肥,健身教练给小胖制定了两个训练方案。方案一:每次连续跑3公里可以消耗300千卡(耗时半小时);方案二:每次连续跑5公里可以消耗600千卡(耗时1小时)。小胖每周周一到周四能抽出半小时跑步，周五到周日能抽出一小时跑步。另外，教练建议小胖每周最多跑21公里，否则会损伤膝盖。请问如果小胖想严格执行教练的训练方案，并且不想损伤膝盖，每周最多通过跑步消耗多少千卡？

• A. 3000
• B. 2400
• C. 2500
• D. 2520

答案：B
解析：设方案1执行x天，方案2执行y天，则有3x+5y<=21 x+y<=7 y<=3。要求 300x+600y 的最大值，枚举可得最优方案为x=2、y=3,此时 300x+600y 为 2400。或使用线性规划亦可求解

二元一次方程组求解

二元一次方程组是一类同时包含两个未知数且每个未知数的次数都是1的线性方程组成的方程组。所谓“二元”指的是方程中有两个未知数，通常记作 $x$ 和 $y$；而“一次”则表示未知数的次数为1。一个典型的二元一次方程组的形式为：

$\begin{aligned} a_1x + b_1y &= c_1 \\ a_2x + b_2y &= c_2 \end{aligned}$

其中，$a_1$、$b_1$、$c_1$、$a_2$、$b_2$、$c_2$ 都是常数，$x$ 和 $y$ 是未知数。

解二元一次方程组的方法

有多种方法可以解二元一次方程组，常用的有以下几种：

1. 代入法

代入法的基本思路是先通过一个方程将一个未知数表示为另一个未知数的表达式，然后将这个表达式代入另一个方程中，消去一个未知数，最后解出另一个未知数。步骤如下：

• 从其中一个方程中解出一个未知数（如 $x$），得到 $x$ 关于 $y$ 的表达式；
• 将这个表达式代入另一个方程中，得到关于 $y$ 的一个方程，解出 $y$；
• 把解出的 $y$ 的值代入第一个方程中，解出 $x$。

例子： 解方程组：

$\begin{aligned} 2x + 3y &= 12 \\ x - y &= 1 \end{aligned}$

• 从第二个方程中解出 $x$： $x = y + 1$；
• 把这个 $x$ 代入第一个方程： $2(y + 1) + 3y = 12$；
• 展开并解出 $y$： $2y + 2 + 3y = 12 \Rightarrow 5y = 10 \Rightarrow y = 2$；
• 把 $y = 2$ 代入 $x = y + 1$： $x = \frac{10}{5} + 1 = 3；
• 因此，解为 $x = 3, y = 2$。

2. 加减法（消元法）

加减法的思路是通过对方程进行加减，消去一个未知数，进而简化为一个一元一次方程。步骤如下：

• 如果两个方程的某个未知数的系数不相等，则可以通过乘以适当的倍数，使其系数相等；
• 然后相加或相减两个方程，消去一个未知数；
• 解出剩下的未知数后，将其代入其中一个原方程，解出另一个未知数。

例子： 解方程组：

$\begin{aligned} 2x + 3y &= 12 \\ x - y &= 1 \end{aligned}$

• 将第二个方程乘以2，使 $x$ 的系数相同： $2(x - y) = 2 \Rightarrow 2x - 2y = 2$；
• 用第一个方程减去这个新的方程： $ (2x + 3y) - (2x - 2y) = 12 - 2 \Rightarrow 5y = 10 \Rightarrow y = 2$；
• 把 $y = 2$ 代入 $x - y = 1$： $x - 2 = 1 \Rightarrow x = 3$；
• 因此，解为 $x = 3, y = 2$。

3. 行列式法（克拉默法则）

行列式法适用于二元一次方程组的一般形式。首先需要计算方程组对应的系数矩阵的行列式，并根据克拉默法则求解。其步骤包括：

• 写出方程组的系数矩阵；
• 计算系数矩阵的行列式；
• 通过替换法则，求解 $x$ 和 $y$。

4. 图解法

图解法是通过在直角坐标系中画出每个方程对应的直线，寻找两条直线的交点。交点的坐标就是方程组的解。这种方法直观，但仅适用于比较简单的方程组。

二元一次方程组的解的分类

根据方程组的解，二元一次方程组可以分为以下几种情况：

1. 唯一解：两条直线相交于一点时，方程组有唯一解。这对应于方程组的行列式不为零。
2. 无解：两条直线平行且没有交点时，方程组无解。
3. 无穷多解：两条直线重合时，方程组有无穷多解。

---

12. 一副纸牌除掉大小王有52张牌，四种花色，每种花色 13 张。假设从这 52 张牌中随机抽取13张纸牌，则至少( )张牌的花色一致

• A. 4
• B. 2
• C. 5
• D. 3

答案：A
解析：

• 这是一个典型的组合问题，利用鸽巢原理（也称为抽屉原理）来解答。

• 鸽巢原理的基本思想是：如果 $n$ 只鸽子被放到 $m$ 个鸽笼中，并且 $n > m$，那么至少有一个鸽笼里有多于一只鸽子。

• 在这道题目中：

  • 共有 4 种花色（4个“鸽笼”），每种花色有 13 张牌。
  • 从52张牌中随机抽取13张牌（13张“鸽子”）。

• 如果我们希望尽量少的牌有相同的花色，那么我们可以将13张牌分配到不同的花色中。我们最多可以给每种花色发3张牌（共 $4 \times 3 = 12$ 张），剩下的1张牌必须分配到某个花色中。因此，至少有一个花色会有4张牌。

• 所以，至少有4张牌的花色是相同的，因此答案为：A. 4

---

13. 一些数字可以颠倒过来看，例如0、1、8颠倒过来还是本身，6颠倒过来是9，9颠倒过来看还是6，其他数字颠倒过来都不构成数字。类似的，一些多位数也可以颠倒过来看，比如106颠倒过来是901。假设某个城市的车牌只由5位数字组成，每一位都可以取0到9。请问这个城市最多有多少个车牌倒过来恰好还是原来的车牌?( )

• A. 60
• B. 125
• C. 100
• D. 75

答案：D
解析：

1. 可用的数字及其倒置映射：

   • 对称数字（倒过来仍然是自己）： 0、1、8
   • 成对数字（倒过来互相变换）： 6↔9，9↔6

   其他数字（2、3、4、5、7）倒过来后不构成合法的数字，不能使用。

2. 车牌号码的结构：

   • 车牌为 5 位数字，每一位可以是 0 到 9 之间的数字（在我们的可用数字范围内）。
   • 为了使车牌倒过来恰好还是原来的车牌，车牌需要是一个 旋转对称数（也称为“上下对称数”或“180 度对称数”）。

3. 旋转对称数的构造：

   • 位置对应关系：

     • 第一位（最左边）与 第五位（最右边）对应。
     • 第二位与 第四位对应。
     • 第三位（中间位）需要自身对称。

   • 位置 1 和位置 5：

     • 可用的数字对为：
       • (0,0)
       • (1,1)
       • (8,8)
       • (6,9)
       • (9,6)
     • 注意： 第一位不能是 0，因为车牌号码不能以 0 开头。然而，题目并未明确限制车牌不能以 0 开头，所以我们暂时保留 0 作为可能的选择。

   • 位置 2 和位置 4：

     • 可用的数字对与位置 1 和位置 5 相同，共有 5 种可能。

   • 位置 3：

     • 只能是对称数字 0、1、8，共有 3 种可能。

4. 总的组合数计算：

   • 位置 1 和位置 5： 5 种可能的数字对。

   • 位置 2 和位置 4： 5 种可能的数字对。

   • 位置 3： 3 种可能的数字。

   • 总的组合数：

     \text{总数} = 5 \times 5 \times 3 = 75

5. 结论：

   • 这个城市最多有 75 个车牌倒过来恰好还是原来的车牌。

所以，正确答案是：

D. 75

---

14. 假设一棵二叉树的后序遍历序列为DGJHEBIFCA,中序遍历序列为DBGEHJACIF则其前序遍历序列为( )

• A. ABDEGJHCFI
• B. ABDEGHJFIC
• C. ABCDEFGHIJ
• D. ABDEGHJCFI

答案：D
解析：后序遍历的规则是“左右根”、中序遍历的规则是“左根右”，因此可知， A是树根DBGEHJ是A左子树的中序遍历(对应后续遍历 DGJHEB)、CIF 是A右子树的中序遍历(对应后续遍历 IFC),递归画出对应的二叉树，再根据前序遍历规则“根左右”即可求出答案

---

15. 以下哪个奖项是计算机科学领域的最高奖?( )

• A. 鲁班奖
• B. 普利策奖
• C. 图灵奖
• D. 诺贝尔奖

答案：C 解析：图灵奖是计算机科学领域的最高奖项，是由计算机协会（ACM）颁发的。